Online Continual Learning for Time Series: a Natural Score-driven Approach

Online continual learning (OCL) methods adapt to changing environments without forgetting past knowledge. Similarly, online time series forecasting (OTSF) is a real-world problem where data evolve in time and success depends on both rapid adaptation and long-term memory. Indeed, time-varying and regime-switching forecasting models have been extensively studied, offering a strong justification for the use of OCL in these settings. Building on recent work that applies OCL to OTSF, this paper aims to strengthen the theoretical and practical connections between time series methods and OCL. First, we reframe neural network optimization as a parameter filtering problem, showing that natural gradient descent is a score-driven method and proving its information-theoretic optimality. Then, we show that using a Student's t likelihood in addition to natural gradient induces a bounded update, which improves robustness to outliers. Finally, we introduce Natural Score-driven Replay (NatSR), which combines our robust optimizer with a replay buffer and a dynamic scale heuristic that improves fast adaptation at regime drifts. Empirical results demonstrate that NatSR achieves stronger forecasting performance than more complex state-of-the-art methods.

Bayesian Autoregressive Online Change-Point Detection with Time-Varying Parameters

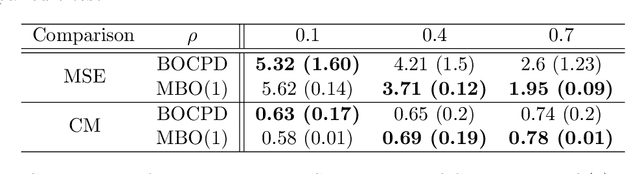
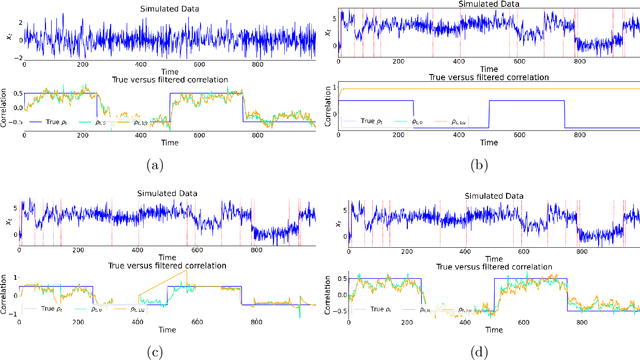
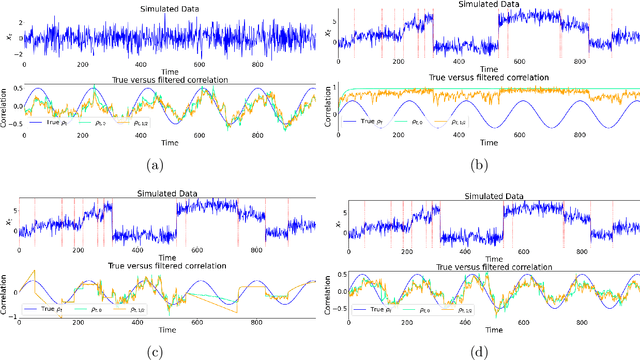
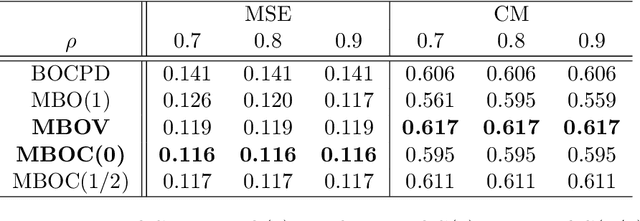
Change points in real-world systems mark significant regime shifts in system dynamics, possibly triggered by exogenous or endogenous factors. These points define regimes for the time evolution of the system and are crucial for understanding transitions in financial, economic, social, environmental, and technological contexts. Building upon the Bayesian approach introduced in \cite{c:07}, we devise a new method for online change point detection in the mean of a univariate time series, which is well suited for real-time applications and is able to handle the general temporal patterns displayed by data in many empirical contexts. We first describe time series as an autoregressive process of an arbitrary order. Second, the variance and correlation of the data are allowed to vary within each regime driven by a scoring rule that updates the value of the parameters for a better fit of the observations. Finally, a change point is detected in a probabilistic framework via the posterior distribution of the current regime length. By modeling temporal dependencies and time-varying parameters, the proposed approach enhances both the estimate accuracy and the forecasting power. Empirical validations using various datasets demonstrate the method's effectiveness in capturing memory and dynamic patterns, offering deeper insights into the non-stationary dynamics of real-world systems.