One-Step Estimation of Differentiable Hilbert-Valued Parameters

We present estimators for smooth Hilbert-valued parameters, where smoothness is characterized by a pathwise differentiability condition. When the parameter space is a reproducing kernel Hilbert space, we provide a means to obtain efficient, root-n rate estimators and corresponding confidence sets. These estimators correspond to generalizations of cross-fitted one-step estimators based on Hilbert-valued efficient influence functions. We give theoretical guarantees even when arbitrary estimators of nuisance functions are used, including those based on machine learning techniques. We show that these results naturally extend to Hilbert spaces that lack a reproducing kernel, as long as the parameter has an efficient influence function. However, we also uncover the unfortunate fact that, when there is no reproducing kernel, many interesting parameters fail to have an efficient influence function, even though they are pathwise differentiable. To handle these cases, we propose a regularized one-step estimator and associated confidence sets. We also show that pathwise differentiability, which is a central requirement of our approach, holds in many cases. Specifically, we provide multiple examples of pathwise differentiable parameters and develop corresponding estimators and confidence sets. Among these examples, four are particularly relevant to ongoing research by the causal inference community: the counterfactual density function, dose-response function, conditional average treatment effect function, and counterfactual kernel mean embedding.

Adversarial Monte Carlo Meta-Learning of Optimal Prediction Procedures

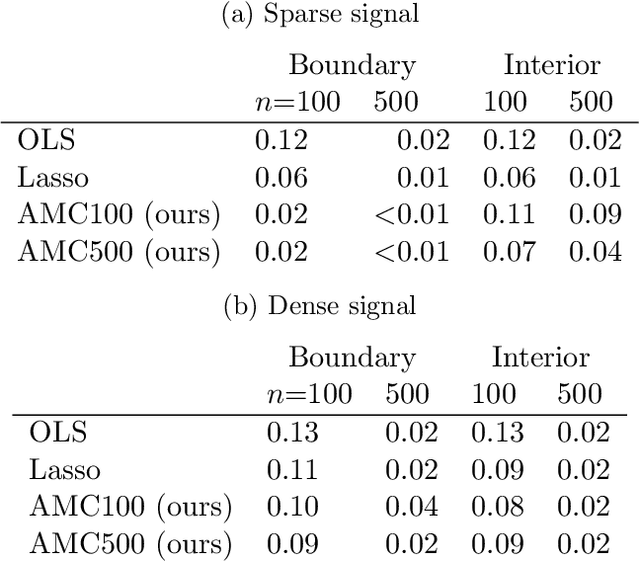
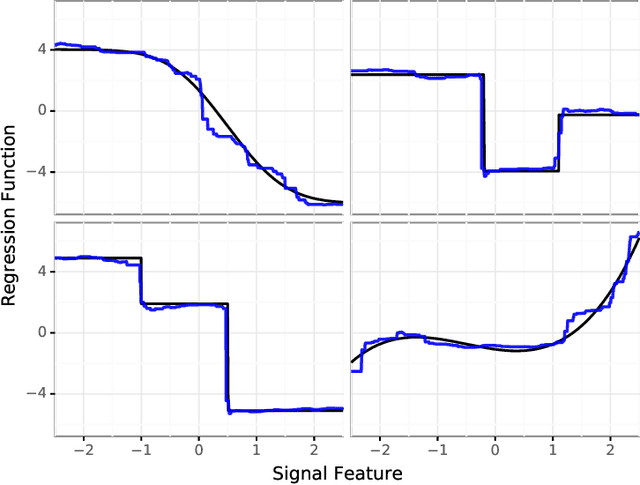
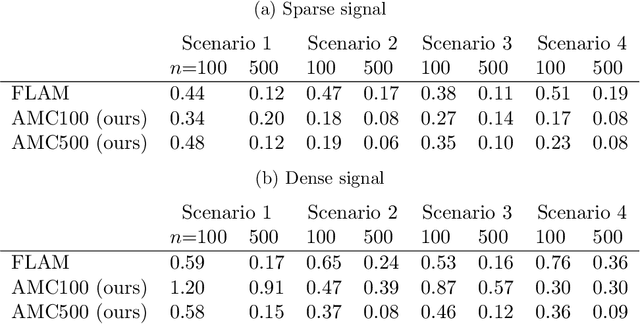
We frame the meta-learning of prediction procedures as a search for an optimal strategy in a two-player game. In this game, Nature selects a prior over distributions that generate labeled data consisting of features and an associated outcome, and the Predictor observes data sampled from a distribution drawn from this prior. The Predictor's objective is to learn a function that maps from a new feature to an estimate of the associated outcome. We establish that, under reasonable conditions, the Predictor has an optimal strategy that is equivariant to shifts and rescalings of the outcome and is invariant to permutations of the observations and to shifts, rescalings, and permutations of the features. We introduce a neural network architecture that satisfies these properties. The proposed strategy performs favorably compared to standard practice in both parametric and nonparametric experiments.