Adversarial Monte Carlo Meta-Learning of Optimal Prediction Procedures
Paper and Code
Feb 26, 2020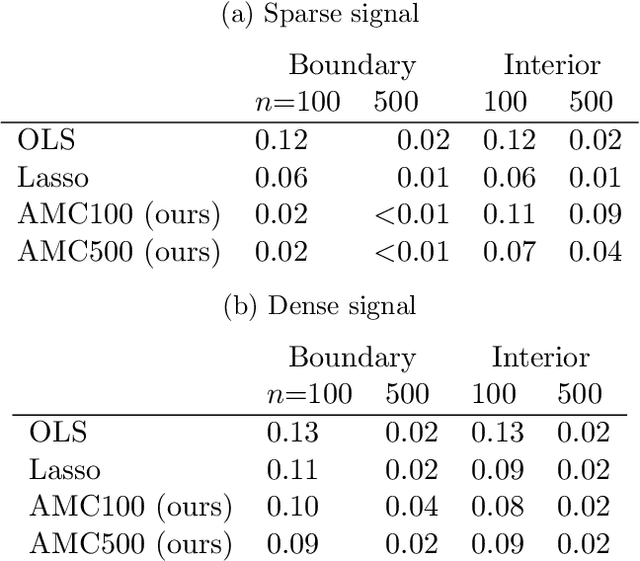
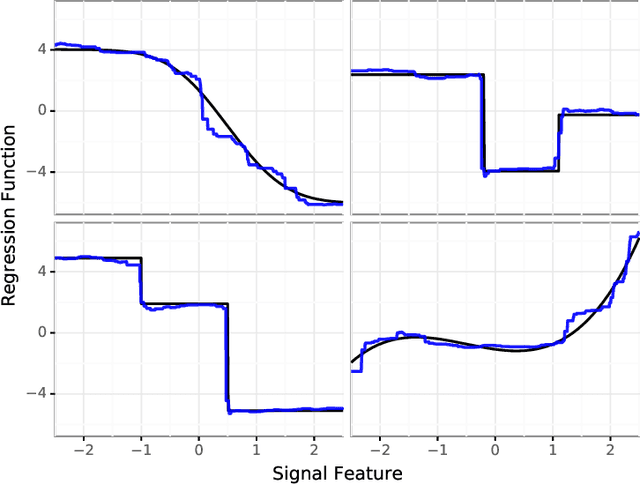
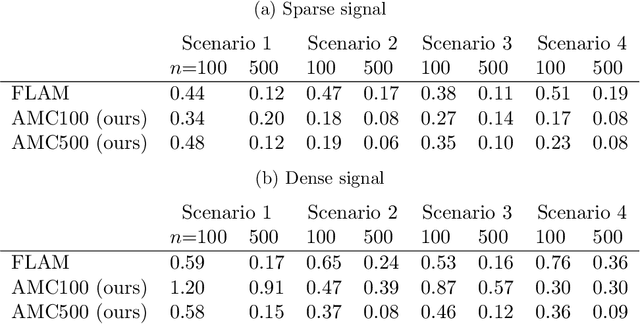
We frame the meta-learning of prediction procedures as a search for an optimal strategy in a two-player game. In this game, Nature selects a prior over distributions that generate labeled data consisting of features and an associated outcome, and the Predictor observes data sampled from a distribution drawn from this prior. The Predictor's objective is to learn a function that maps from a new feature to an estimate of the associated outcome. We establish that, under reasonable conditions, the Predictor has an optimal strategy that is equivariant to shifts and rescalings of the outcome and is invariant to permutations of the observations and to shifts, rescalings, and permutations of the features. We introduce a neural network architecture that satisfies these properties. The proposed strategy performs favorably compared to standard practice in both parametric and nonparametric experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge