PAC-Net: A Model Pruning Approach to Inductive Transfer Learning

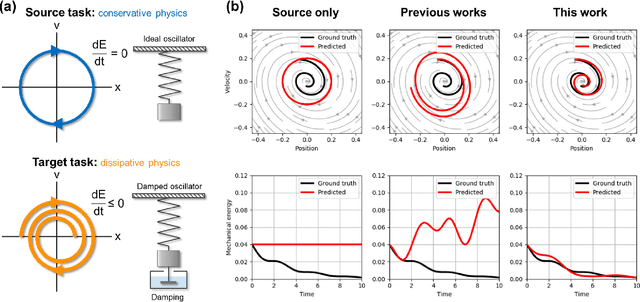
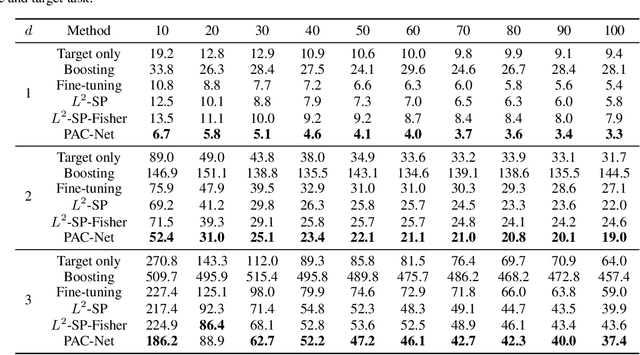
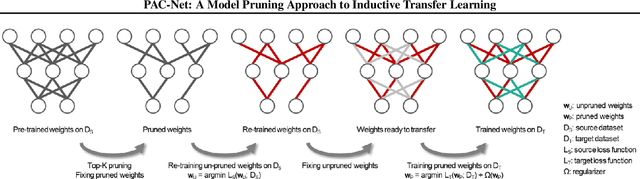
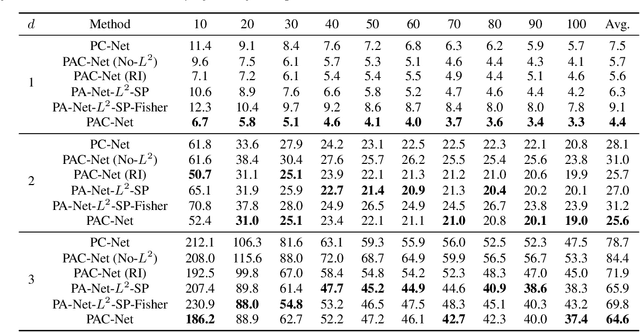
Inductive transfer learning aims to learn from a small amount of training data for the target task by utilizing a pre-trained model from the source task. Most strategies that involve large-scale deep learning models adopt initialization with the pre-trained model and fine-tuning for the target task. However, when using over-parameterized models, we can often prune the model without sacrificing the accuracy of the source task. This motivates us to adopt model pruning for transfer learning with deep learning models. In this paper, we propose PAC-Net, a simple yet effective approach for transfer learning based on pruning. PAC-Net consists of three steps: Prune, Allocate, and Calibrate (PAC). The main idea behind these steps is to identify essential weights for the source task, fine-tune on the source task by updating the essential weights, and then calibrate on the target task by updating the remaining redundant weights. Under the various and extensive set of inductive transfer learning experiments, we show that our method achieves state-of-the-art performance by a large margin.

Time-Reversal Symmetric ODE Network

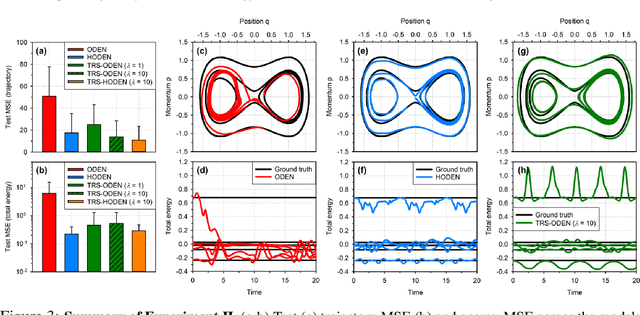
Time-reversal symmetry, which requires that the dynamics of a system should not change with the reversal of time axis, is a fundamental property that frequently holds in classical and quantum mechanics. In this paper, we propose a novel loss function that measures how well our ordinary differential equation (ODE) networks comply with this time-reversal symmetry; it is formally defined by the discrepancy in the time evolution of ODE networks between forward and backward dynamics. Then, we design a new framework, which we name as Time-Reversal Symmetric ODE Networks (TRS-ODENs), that can learn the dynamics of physical systems more sample-efficiently by learning with the proposed loss function. We evaluate TRS-ODENs on several classical dynamics, and find they can learn the desired time evolution from observed noisy and complex trajectories. We also show that, even for systems that do not possess the full time-reversal symmetry, TRS-ODENs can achieve better predictive errors over baselines.