Iheb Nassim Aouadj
LOOPer: A Learned Automatic Code Optimizer For Polyhedral Compilers
Mar 22, 2024



Abstract:While polyhedral compilers have shown success in implementing advanced code transformations, they still have challenges in selecting the most profitable transformations that lead to the best speedups. This has motivated the use of machine learning to build cost models to guide the search for polyhedral optimizations. State-of-the-art polyhedral compilers have demonstrated a viable proof-of-concept of this approach. While such a proof-of-concept has shown promise, it still has significant limitations. State-of-the-art polyhedral compilers that use a deep-learning cost model only support a small subset of affine transformations, limiting their ability to apply complex code transformations. They also only support simple programs that have a single loop nest and a rectangular iteration domain, limiting their applicability to many programs. These limitations significantly impact the generality of such compilers and autoschedulers and put into question the whole approach. In this paper, we introduce LOOPer, the first polyhedral autoscheduler that uses a deep-learning based cost model and covers a large set of affine transformations and programs. It supports the exploration of a large set of affine transformations, allowing the application of complex sequences of polyhedral transformations. It also supports the optimization of programs with multiple loop nests and with rectangular and non-rectangular iteration domains, allowing the optimization of an extensive set of programs. We implement and evaluate LOOPer and show that it achieves speedups over the state-of-the-art. On the Polybench benchmark, LOOPer achieves a geometric mean speedup of 1.59x over Tiramisu. LOOPer also achieves competitive speedups with a geometric mean speedup of 1.34x over Pluto, a state-of-the-art polyhedral compiler that does not use a machine-learning based cost model.
Progress Report: A Deep Learning Guided Exploration of Affine Unimodular Loop Transformations
Jun 08, 2022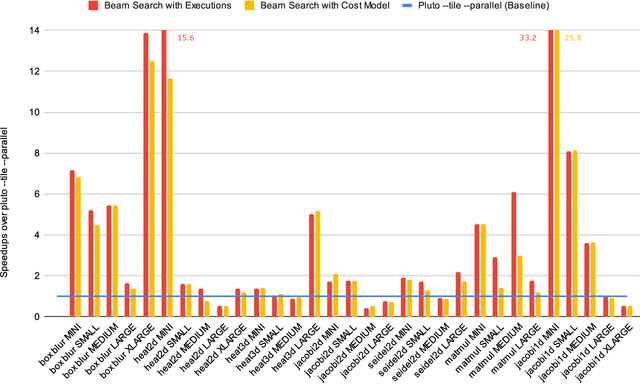
Abstract:In this paper, we present a work in progress about a deep learning based approach for automatic code optimization in polyhedral compilers. The proposed technique explores combinations of affine and non-affine loop transformations to find the sequence of transformations that minimizes the execution time of a given program. This exploration is guided by a deep learning based cost model that evaluates the speedup that each sequence of transformations would yield. Preliminary results show that the proposed techniques achieve a 2.35x geometric mean speedup over state of the art polyhedral compilers (Pluto).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge