Non-FPT lower bounds for structural restrictions of decision DNNF

We give a non-FPT lower bound on the size of structured decision DNNF and OBDD with decomposable AND-nodes representing CNF-formulas of bounded incidence treewidth. Both models are known to be of FPT size for CNFs of bounded primal treewidth. To the best of our knowledge this is the first parameterized separation of primal treewidth and incidence treewidth for knowledge compilation models.

On oblivious branching programs with bounded repetition that cannot efficiently compute CNFs of bounded treewidth

In this paper we study complexity of an extension of ordered binary decision diagrams (OBDDs) called $c$-OBDDs on CNFs of bounded (primal graph) treewidth. In particular, we show that for each $k$ there is a class of CNFs of treewidth $k \geq 3$ for which the equivalent $c$-OBDDs are of size $\Omega(n^{k/(8c-4)})$. Moreover, this lower bound holds if $c$-OBDD is non-deterministic and semantic. Our second result uses the above lower bound to separate the above model from sentential decision diagrams (SDDs). In order to obtain the lower bound, we use a structural graph parameter called matching width. Our third result shows that matching width and pathwidth are linearly related.

On the read-once property of branching programs and CNFs of bounded treewidth

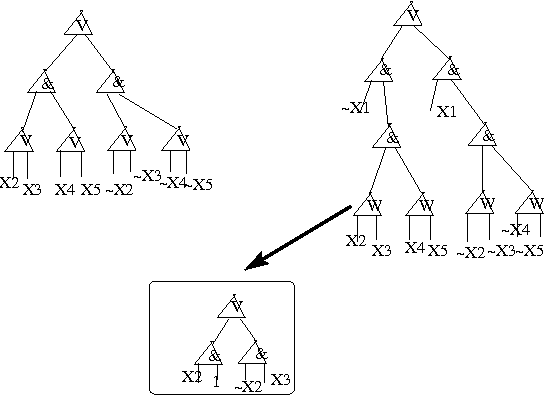
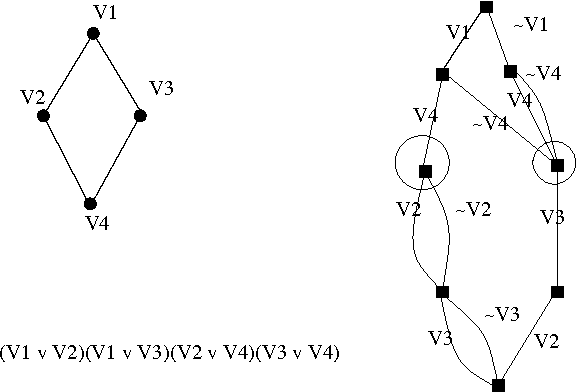
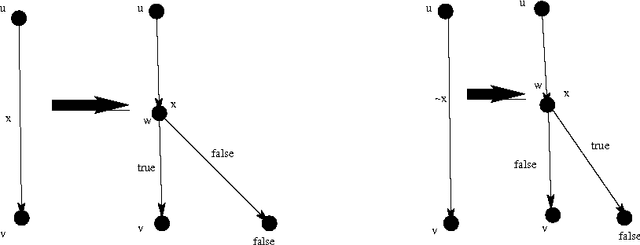
In this paper we prove a space lower bound of $n^{\Omega(k)}$ for non-deterministic (syntactic) read-once branching programs ({\sc nrobp}s) on functions expressible as {\sc cnf}s with treewidth at most $k$ of their primal graphs. This lower bound rules out the possibility of fixed-parameter space complexity of {\sc nrobp}s parameterized by $k$. We use lower bound for {\sc nrobp}s to obtain a quasi-polynomial separation between Free Binary Decision Diagrams and Decision Decomposable Negation Normal Forms, essentially matching the existing upper bound introduced by Beame et al. and thus proving the tightness of the latter.

Soft Constraints of Difference and Equality

In many combinatorial problems one may need to model the diversity or similarity of assignments in a solution. For example, one may wish to maximise or minimise the number of distinct values in a solution. To formulate problems of this type, we can use soft variants of the well known AllDifferent and AllEqual constraints. We present a taxonomy of six soft global constraints, generated by combining the two latter ones and the two standard cost functions, which are either maximised or minimised. We characterise the complexity of achieving arc and bounds consistency on these constraints, resolving those cases for which NP-hardness was neither proven nor disproven. In particular, we explore in depth the constraint ensuring that at least k pairs of variables have a common value. We show that achieving arc consistency is NP-hard, however achieving bounds consistency can be done in polynomial time through dynamic programming. Moreover, we show that the maximum number of pairs of equal variables can be approximated by a factor 1/2 with a linear time greedy algorithm. Finally, we provide a fixed parameter tractable algorithm with respect to the number of values appearing in more than two distinct domains. Interestingly, this taxonomy shows that enforcing equality is harder than enforcing difference.