On the read-once property of branching programs and CNFs of bounded treewidth
Paper and Code
Jul 26, 2015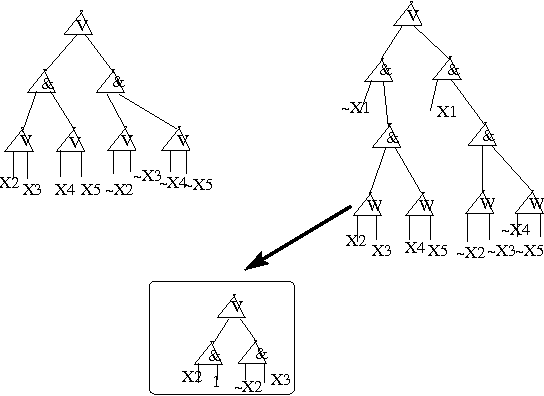
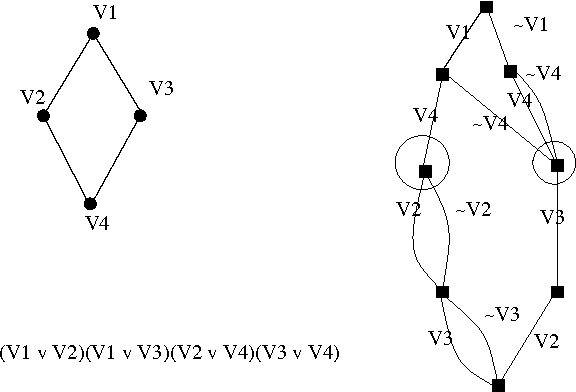

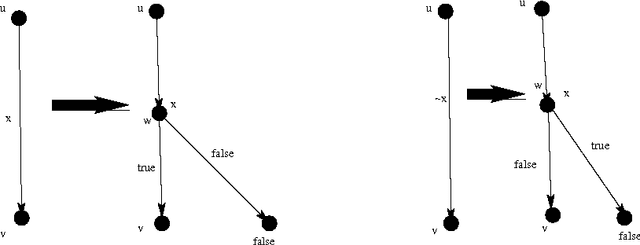
In this paper we prove a space lower bound of $n^{\Omega(k)}$ for non-deterministic (syntactic) read-once branching programs ({\sc nrobp}s) on functions expressible as {\sc cnf}s with treewidth at most $k$ of their primal graphs. This lower bound rules out the possibility of fixed-parameter space complexity of {\sc nrobp}s parameterized by $k$. We use lower bound for {\sc nrobp}s to obtain a quasi-polynomial separation between Free Binary Decision Diagrams and Decision Decomposable Negation Normal Forms, essentially matching the existing upper bound introduced by Beame et al. and thus proving the tightness of the latter.
* Significantly simplified proof of the main combinatorial lemma.
AROSRN replaced back by NROBP due to their equivalence
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge