Better Best of Both Worlds Bounds for Bandits with Switching Costs

We study best-of-both-worlds algorithms for bandits with switching cost, recently addressed by Rouyer, Seldin and Cesa-Bianchi, 2021. We introduce a surprisingly simple and effective algorithm that simultaneously achieves minimax optimal regret bound of $\mathcal{O}(T^{2/3})$ in the oblivious adversarial setting and a bound of $\mathcal{O}(\min\{\log (T)/\Delta^2,T^{2/3}\})$ in the stochastically-constrained regime, both with (unit) switching costs, where $\Delta$ is the gap between the arms. In the stochastically constrained case, our bound improves over previous results due to Rouyer et al., that achieved regret of $\mathcal{O}(T^{1/3}/\Delta)$. We accompany our results with a lower bound showing that, in general, $\tilde{\Omega}(\min\{1/\Delta^2,T^{2/3}\})$ regret is unavoidable in the stochastically-constrained case for algorithms with $\mathcal{O}(T^{2/3})$ worst-case regret.

Thinking Outside the Ball: Optimal Learning with Gradient Descent for Generalized Linear Stochastic Convex Optimization

We consider linear prediction with a convex Lipschitz loss, or more generally, stochastic convex optimization problems of generalized linear form, i.e.~where each instantaneous loss is a scalar convex function of a linear function. We show that in this setting, early stopped Gradient Descent (GD), without any explicit regularization or projection, ensures excess error at most $\epsilon$ (compared to the best possible with unit Euclidean norm) with an optimal, up to logarithmic factors, sample complexity of $\tilde{O}(1/\epsilon^2)$ and only $\tilde{O}(1/\epsilon^2)$ iterations. This contrasts with general stochastic convex optimization, where $\Omega(1/\epsilon^4)$ iterations are needed Amir et al. [2021b]. The lower iteration complexity is ensured by leveraging uniform convergence rather than stability. But instead of uniform convergence in a norm ball, which we show can guarantee suboptimal learning using $\Theta(1/\epsilon^4)$ samples, we rely on uniform convergence in a distribution-dependent ball.

Never Go Full Batch (in Stochastic Convex Optimization)

We study the generalization performance of $\text{full-batch}$ optimization algorithms for stochastic convex optimization: these are first-order methods that only access the exact gradient of the empirical risk (rather than gradients with respect to individual data points), that include a wide range of algorithms such as gradient descent, mirror descent, and their regularized and/or accelerated variants. We provide a new separation result showing that, while algorithms such as stochastic gradient descent can generalize and optimize the population risk to within $\epsilon$ after $O(1/\epsilon^2)$ iterations, full-batch methods either need at least $\Omega(1/\epsilon^4)$ iterations or exhibit a dimension-dependent sample complexity.

SGD Generalizes Better Than GD (And Regularization Doesn't Help)

We give a new separation result between the generalization performance of stochastic gradient descent (SGD) and of full-batch gradient descent (GD) in the fundamental stochastic convex optimization model. While for SGD it is well-known that $O(1/\epsilon^2)$ iterations suffice for obtaining a solution with $\epsilon$ excess expected risk, we show that with the same number of steps GD may overfit and emit a solution with $\Omega(1)$ generalization error. Moreover, we show that in fact $\Omega(1/\epsilon^4)$ iterations are necessary for GD to match the generalization performance of SGD, which is also tight due to recent work by Bassily et al. (2020). We further discuss how regularizing the empirical risk minimized by GD essentially does not change the above result, and revisit the concepts of stability, implicit bias and the role of the learning algorithm in generalization.

Prediction with Corrupted Expert Advice

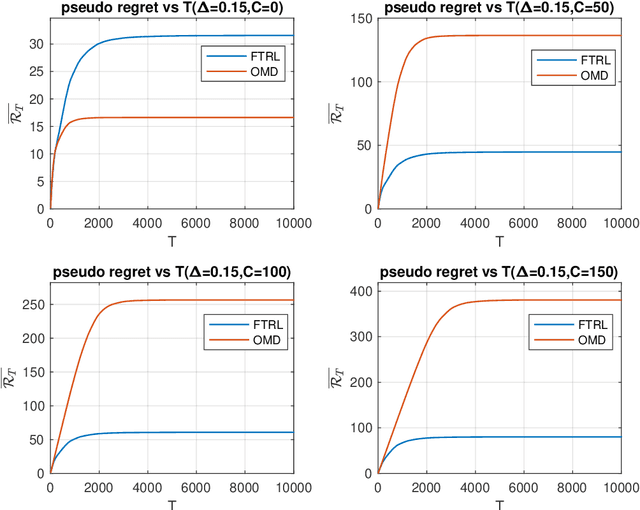
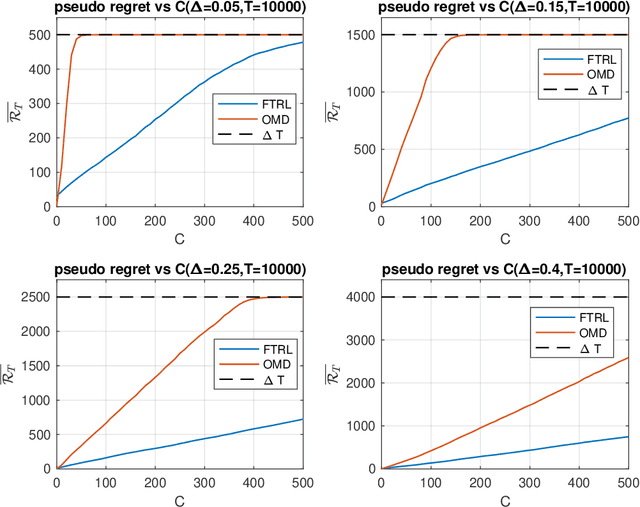
We revisit the fundamental problem of prediction with expert advice, in a setting where the environment is benign and generates losses stochastically, but the feedback observed by the learner is subject to a moderate adversarial corruption. We prove that a variant of the classical Multiplicative Weights algorithm with decreasing step sizes achieves constant regret in this setting and performs optimally in a wide range of environments, regardless of the magnitude of the injected corruption. Our results reveal a surprising disparity between the often comparable Follow the Regularized Leader (FTRL) and Online Mirror Descent (OMD) frameworks: we show that for experts in the corrupted stochastic regime, the regret performance of OMD is in fact strictly inferior to that of FTRL.