Designing Discontinuities

Discontinuities can be fairly arbitrary but also cause a significant impact on outcomes in social systems. Indeed, their arbitrariness is why they have been used to infer causal relationships among variables in numerous settings. Regression discontinuity from econometrics assumes the existence of a discontinuous variable that splits the population into distinct partitions to estimate the causal effects of a given phenomenon. Here we consider the design of partitions for a given discontinuous variable to optimize a certain effect previously studied using regression discontinuity. To do so, we propose a quantization-theoretic approach to optimize the effect of interest, first learning the causal effect size of a given discontinuous variable and then applying dynamic programming for optimal quantization design of discontinuities that balance the gain and loss in the effect size. We also develop a computationally-efficient reinforcement learning algorithm for the dynamic programming formulation of optimal quantization. We demonstrate our approach by designing optimal time zone borders for counterfactuals of social capital, social mobility, and health. This is based on regression discontinuity analyses we perform on novel data, which may be of independent empirical interest in showing a causal relationship between sunset time and social capital.

Learning Optimal Features via Partial Invariance

Learning models that are robust to test-time distribution shifts is a key concern in domain generalization, and in the wider context of their real-life applicability. Invariant Risk Minimization (IRM) is one particular framework that aims to learn deep invariant features from multiple domains and has subsequently led to further variants. A key assumption for the success of these methods requires that the underlying causal mechanisms/features remain invariant across domains and the true invariant features be sufficient to learn the optimal predictor. In practical problem settings, these assumptions are often not satisfied, which leads to IRM learning a sub-optimal predictor for that task. In this work, we propose the notion of partial invariance as a relaxation of the IRM framework. Under our problem setting, we first highlight the sub-optimality of the IRM solution. We then demonstrate how partitioning the training domains, assuming access to some meta-information about the domains, can help improve the performance of invariant models via partial invariance. Finally, we conduct several experiments, both in linear settings as well as with classification tasks in language and images with deep models, which verify our conclusions.

Optimal Recovery for Causal Inference

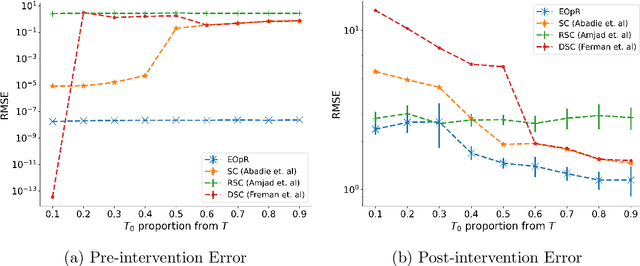
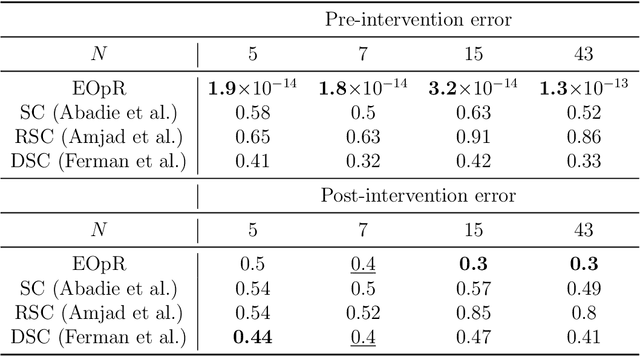
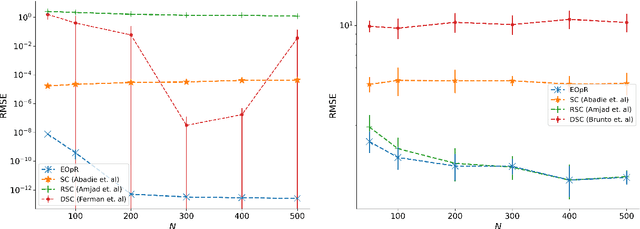
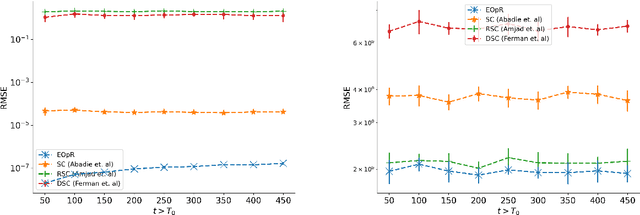
It is crucial to successfully quantify causal effects of a policy intervention to determine whether the policy achieved the desired outcomes. We present a deterministic approach to a classical method of policy evaluation, synthetic control (Abadie and Gardeazabal, 2003), to estimate the unobservable outcome of a treatment unit using ellipsoidal optimal recovery (EOpR). EOpR provides policy evaluators with "worst-case" outcomes and "typical" outcomes to help in decision making. It is an approximation-theoretic technique that also relates to the theory of principal components, which recovers unknown observations given a learned signal class and a set of known observations. We show that EOpR can improve pre-treatment fit and bias of the post-treatment estimation relative to other econometrics methods. Beyond recovery of the unit of interest, an advantage of EOpR is that it produces worst-case estimates over the estimations produced by the recovery. We assess our approach on artificially-generated data, on datasets commonly used in the econometrics literature, and also derive results in the context of the COVID-19 pandemic. Such an approach is novel in the econometrics literature for causality and policy evaluation.

Balancing Fairness and Robustness via Partial Invariance

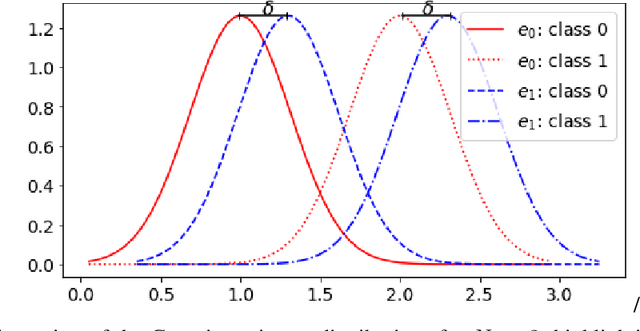
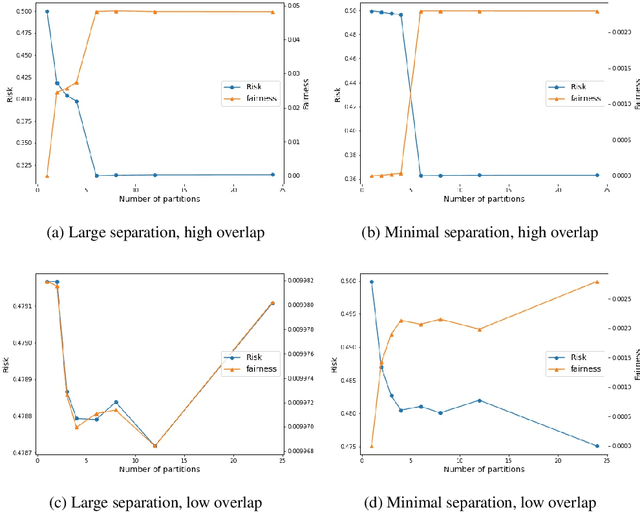
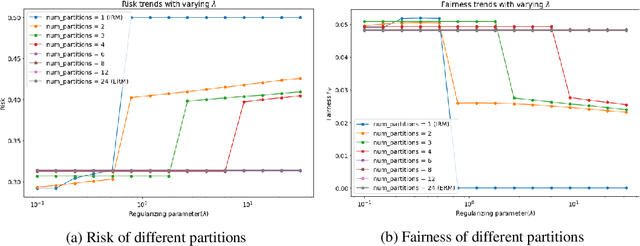
The Invariant Risk Minimization (IRM) framework aims to learn invariant features from a set of environments for solving the out-of-distribution (OOD) generalization problem. The underlying assumption is that the causal components of the data generating distributions remain constant across the environments or alternately, the data "overlaps" across environments to find meaningful invariant features. Consequently, when the "overlap" assumption does not hold, the set of truly invariant features may not be sufficient for optimal prediction performance. Such cases arise naturally in networked settings and hierarchical data-generating models, wherein the IRM performance becomes suboptimal. To mitigate this failure case, we argue for a partial invariance framework. The key idea is to introduce flexibility into the IRM framework by partitioning the environments based on hierarchical differences, while enforcing invariance locally within the partitions. We motivate this framework in classification settings with causal distribution shifts across environments. Our results show the capability of the partial invariant risk minimization to alleviate the trade-off between fairness and risk in certain settings.