Optimal Recovery for Causal Inference
Paper and Code
Aug 13, 2022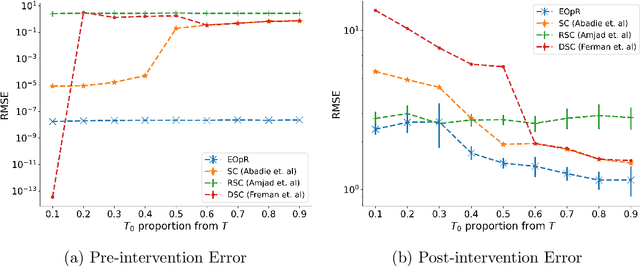
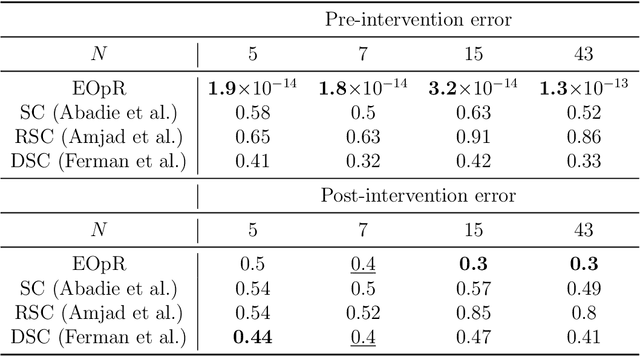
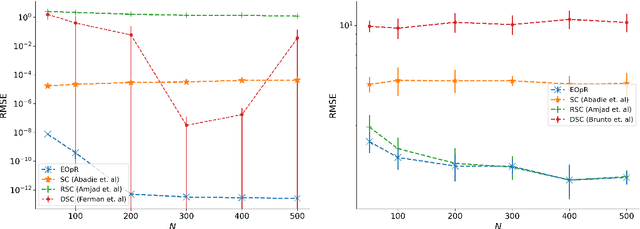
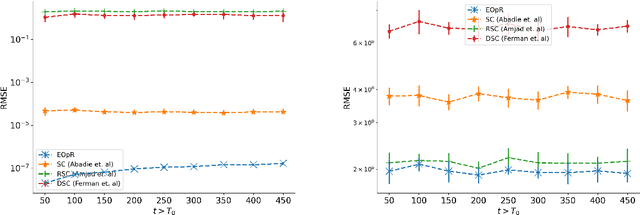
It is crucial to successfully quantify causal effects of a policy intervention to determine whether the policy achieved the desired outcomes. We present a deterministic approach to a classical method of policy evaluation, synthetic control (Abadie and Gardeazabal, 2003), to estimate the unobservable outcome of a treatment unit using ellipsoidal optimal recovery (EOpR). EOpR provides policy evaluators with "worst-case" outcomes and "typical" outcomes to help in decision making. It is an approximation-theoretic technique that also relates to the theory of principal components, which recovers unknown observations given a learned signal class and a set of known observations. We show that EOpR can improve pre-treatment fit and bias of the post-treatment estimation relative to other econometrics methods. Beyond recovery of the unit of interest, an advantage of EOpR is that it produces worst-case estimates over the estimations produced by the recovery. We assess our approach on artificially-generated data, on datasets commonly used in the econometrics literature, and also derive results in the context of the COVID-19 pandemic. Such an approach is novel in the econometrics literature for causality and policy evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge