Ibai Roman
Evolving Gaussian Process kernels from elementary mathematical expressions
Oct 14, 2019
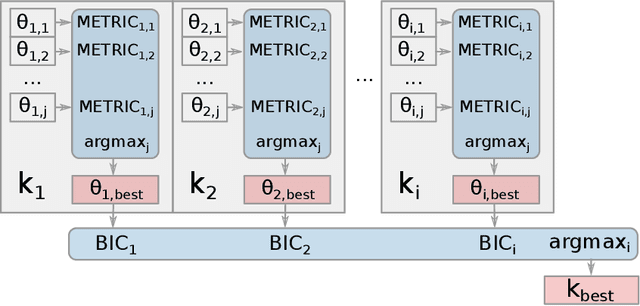
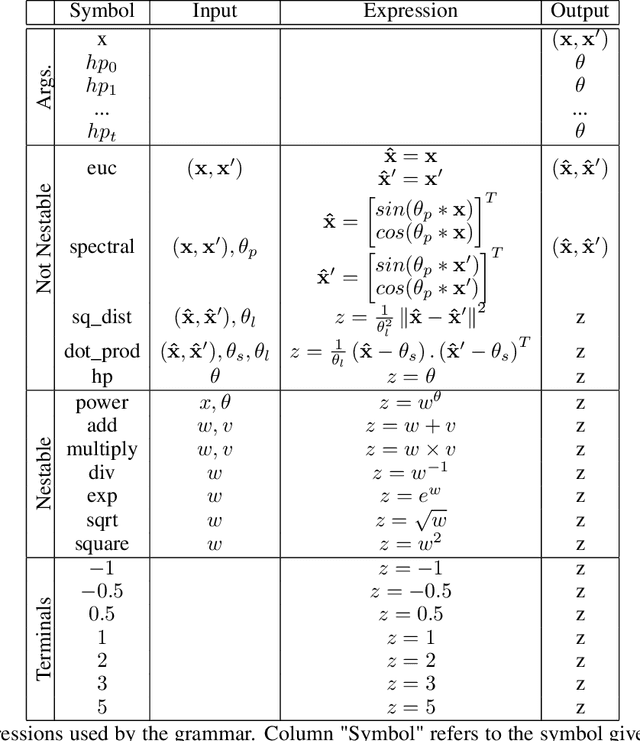
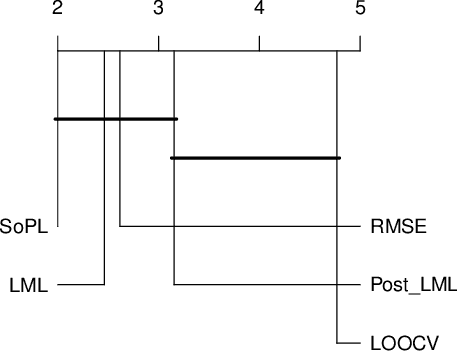
Abstract:Choosing the most adequate kernel is crucial in many Machine Learning applications. Gaussian Process is a state-of-the-art technique for regression and classification that heavily relies on a kernel function. However, in the Gaussian Process literature, kernels have usually been either ad hoc designed, selected from a predefined set, or searched for in a space of compositions of kernels which have been defined a priori. In this paper, we propose a Genetic-Programming algorithm that represents a kernel function as a tree of elementary mathematical expressions. By means of this representation, a wider set of kernels can be modeled, where potentially better solutions can be found, although new challenges also arise. The proposed algorithm is able to overcome these difficulties and find kernels that accurately model the characteristics of the data. This method has been tested in several real-world time-series extrapolation problems, improving the state-of-the-art results while reducing the complexity of the kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge