Classical and Quantum Algorithms for the Deterministic L-system Inductive Inference Problem

L-systems can be made to model and create simulations of many biological processes, such as plant development. Finding an L-system for a given process is typically solved by hand, by experts, in a hugely time-consuming process. It would be significant if this could be done automatically from data, such as from sequences of images. In this paper, we are interested in inferring a particular type of L-system, deterministic context-free L-system (D0L-system) from a sequence of strings. We introduce the characteristic graph of a sequence of strings, which we then utilize to translate our problem (inferring D0L-system) in polynomial time into the maximum independent set problem (MIS) and the SAT problem. After that, we offer a classical exact algorithm and an approximate quantum algorithm for the problem.

Optimal L-Systems for Stochastic L-system Inference Problems

This paper presents two novel theorems that address two open problems in stochastic Lindenmayer-system (L-system) inference, specifically focusing on the construction of an optimal stochastic L-system capable of generating a given sequence of strings. The first theorem delineates a method for crafting a stochastic L-system that maximizes the likelihood of producing a given sequence of words through a singular derivation. Furthermore, the second theorem determines the stochastic L-systems with the highest probability of producing a given sequence of words with multiple possible derivations. From these, we introduce an algorithm to infer an optimal stochastic L-system from a given sequence. This algorithm incorporates sophisticated optimization techniques, such as interior point methods, ensuring production of a stochastically optimal stochastic L-system suitable for generating the given sequence. This allows for the use of using stochastic L-systems as model for machine learning using only positive data for training.

Improving Deep Learning Predictions with Simulated Images, and Vice Versa

Artificial neural networks are often used to identify features of crop plants. However, training their models requires many annotated images, which can be expensive and time-consuming to acquire. Procedural models of plants, such as those developed with Lindenmayer-systems (L-systems) can be created to produce visually realistic simulations, and hence images of plant simulations, where annotations are implicitly known. These synthetic images can either augment or completely replace real images in training neural networks for phenotyping tasks. In this paper, we systematically vary amounts of real and synthetic images used for training in both maize and canola to better understand situations where synthetic images generated from L-systems can help prediction on real images. This work also explores the degree to which realism in the synthetic images improves prediction. Furthermore, we see how neural network predictions can be used to help calibrate L-systems themselves, creating a feedback loop.

A Novel Technique Combining Image Processing, Plant Development Properties, and the Hungarian Algorithm, to Improve Leaf Detection in Maize

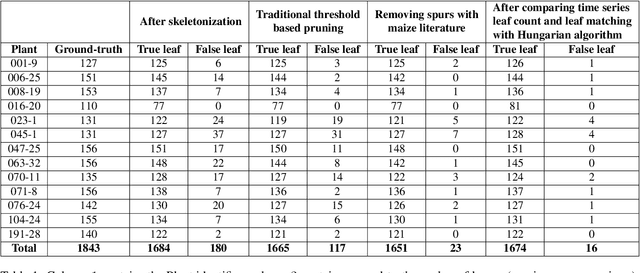
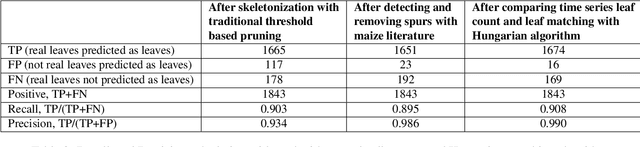
Manual determination of plant phenotypic properties such as plant architecture, growth, and health is very time consuming and sometimes destructive. Automatic image analysis has become a popular approach. This research aims to identify the position (and number) of leaves from a temporal sequence of high-quality indoor images consisting of multiple views, focussing in particular of images of maize. The procedure used a segmentation on the images, using the convex hull to pick the best view at each time step, followed by a skeletonization of the corresponding image. To remove skeleton spurs, a discrete skeleton evolution pruning process was applied. Pre-existing statistics regarding maize development was incorporated to help differentiate between true leaves and false leaves. Furthermore, for each time step, leaves were matched to those of the previous and next three days using the graph-theoretic Hungarian algorithm. This matching algorithm can be used to both remove false positives, and also to predict true leaves, even if they were completely occluded from the image itself. The algorithm was evaluated using an open dataset consisting of 13 maize plants across 27 days from two different views. The total number of true leaves from the dataset was 1843, and our proposed techniques detect a total of 1690 leaves including 1674 true leaves, and only 16 false leaves, giving a recall of 90.8%, and a precision of 99.0%.

DNA Methylation Data to Predict Suicidal and Non-Suicidal Deaths: A Machine Learning Approach

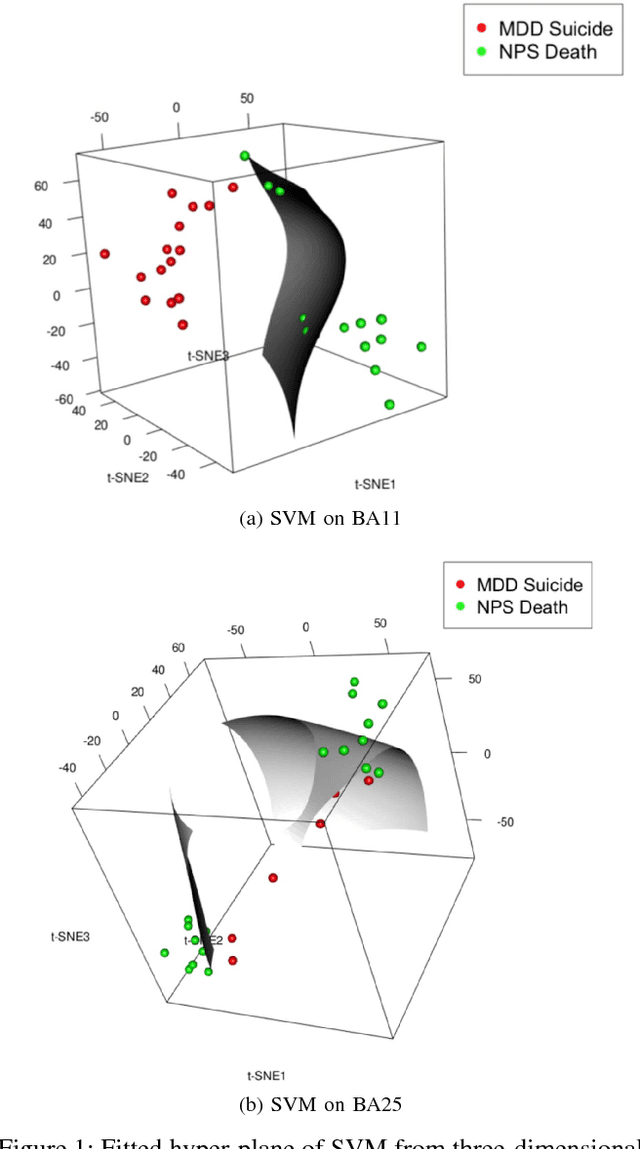
The objective of this study is to predict suicidal and non-suicidal deaths from DNA methylation data using a modern machine learning algorithm. We used support vector machines to classify existing secondary data consisting of normalized values of methylated DNA probe intensities from tissues of two cortical brain regions to distinguish suicide cases from control cases. Before classification, we employed Principal component analysis (PCA) and t-distributed Stochastic Neighbor Embedding (t-SNE) to reduce the dimension of the data. In comparison to PCA, the modern data visualization method t-SNE performs better in dimensionality reduction. t-SNE accounts for the possible non-linear patterns in low-dimensional data. We applied four-fold cross-validation in which the resulting output from t-SNE was used as training data for the Support Vector Machine (SVM). Despite the use of cross-validation, the nominally perfect prediction of suicidal deaths for BA11 data suggests possible over-fitting of the model. The study also may have suffered from 'spectrum bias' since the individuals were only studied from two extreme scenarios. This research constitutes a baseline study for classifying suicidal and non-suicidal deaths from DNA methylation data. Future studies with larger sample size, while possibly incorporating methylation data from living individuals, may reduce the bias and improve the accuracy of the results.

Stochastic L-system Inference from Multiple String Sequence Inputs

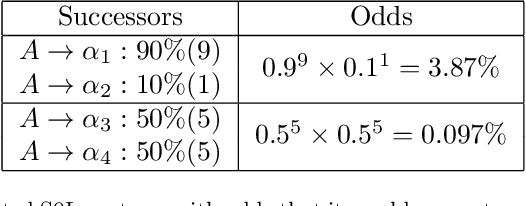
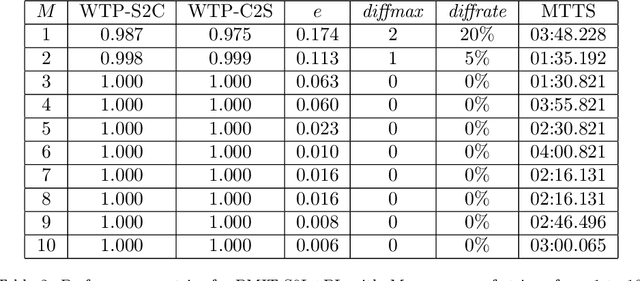
Lindenmayer systems (L-systems) are a grammar system that consist of string rewriting rules. The rules replace every symbol in a string in parallel with a successor to produce the next string, and this procedure iterates. In a stochastic context-free L-system (S0L-system), every symbol may have one or more rewriting rule, each with an associated probability of selection. Properly constructed rewriting rules have been found to be useful for modeling and simulating some natural and human engineered processes where each derived string describes a step in the simulation. Typically, processes are modeled by experts who meticulously construct the rules based on measurements or domain knowledge of the process. This paper presents an automated approach to finding stochastic L-systems, given a set of string sequences as input. The implemented tool is called the Plant Model Inference Tool for S0L-systems (PMIT-S0L). PMIT-S0L is evaluated using 960 procedurally generated S0L-systems in a test suite, which are each used to generate input strings, and PMIT-S0L is then used to infer the system from only the sequences. The evaluation shows that PMIT-S0L infers S0L-systems with up to 9 rewriting rules each in under 12 hours. Additionally, it is found that 3 sequences of strings is sufficient to find the correct original rewriting rules in 100% of the cases in the test suite, and 6 sequences of strings reduces the difference in the associated probabilities to approximately 1% or less.

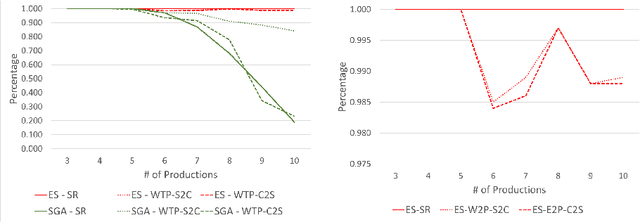
New Techniques for Inferring L-Systems Using Genetic Algorithm

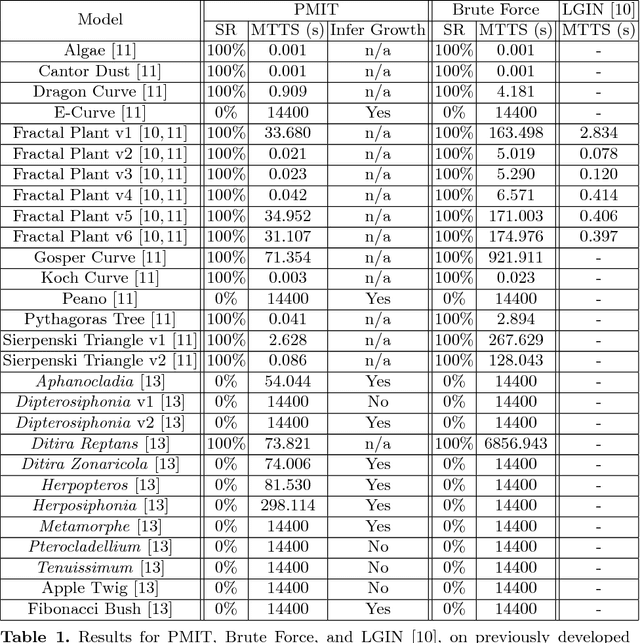
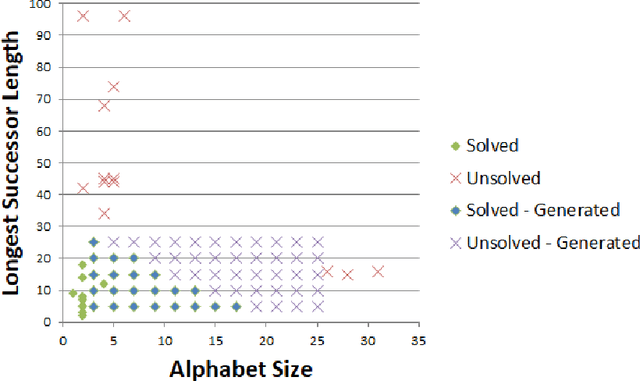
Lindenmayer systems (L-systems) are a formal grammar system that iteratively rewrites all symbols of a string, in parallel. When visualized with a graphical interpretation, the images have self-similar shapes that appear frequently in nature, and they have been particularly successful as a concise, reusable technique for simulating plants. The L-system inference problem is to find an L-system to simulate a given plant. This is currently done mainly by experts, but this process is limited by the availability of experts, the complexity that may be solved by humans, and time. This paper introduces the Plant Model Inference Tool (PMIT) that infers deterministic context-free L-systems from an initial sequence of strings generated by the system using a genetic algorithm. PMIT is able to infer more complex systems than existing approaches. Indeed, while existing approaches are limited to L-systems with a total sum of 20 combined symbols in the productions, PMIT can infer almost all L-systems tested where the total sum is 140 symbols. This was validated using a test bed of 28 previously developed L-system models, in addition to models created artificially by bootstrapping larger models.