Automated Grading of Anatomical Objective Structured Practical Exams Using Decision Trees

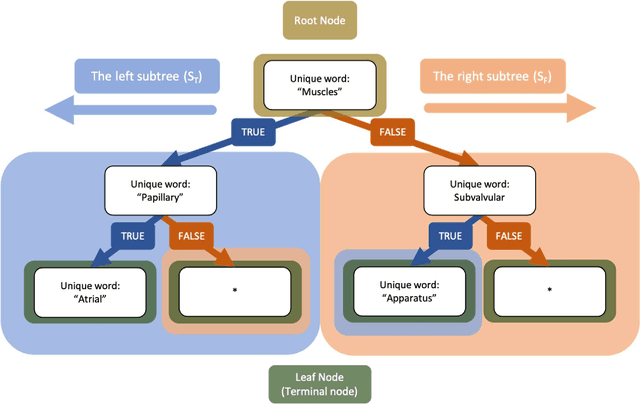
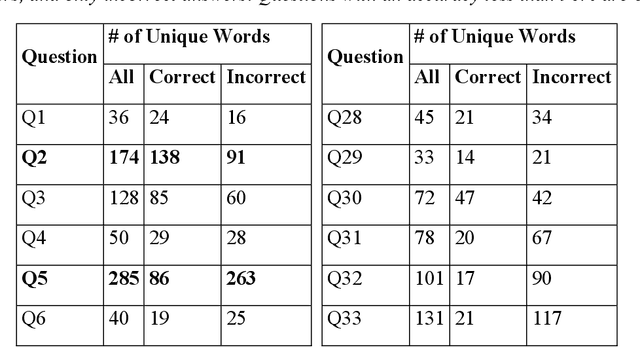
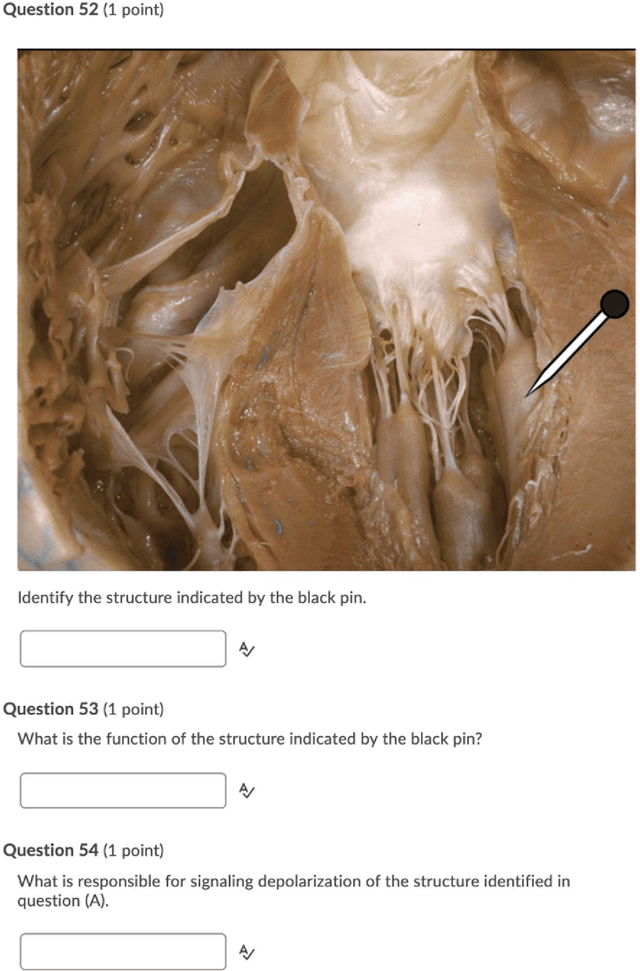
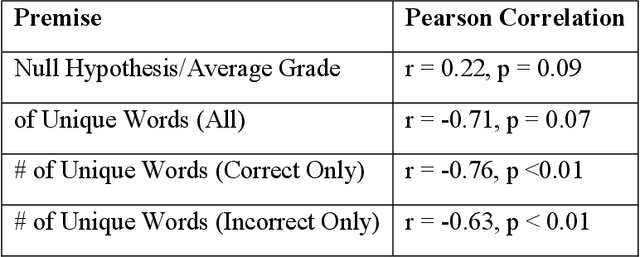
An Objective Structured Practical Examination (OSPE) is an effective and robust, but resource-intensive, means of evaluating anatomical knowledge. Since most OSPEs employ short answer or fill-in-the-blank style questions, the format requires many people familiar with the content to mark the exams. However, the increasing prevalence of online delivery for anatomy and physiology courses could result in students losing the OSPE practice that they would receive in face-to-face learning sessions. The purpose of this study was to test the accuracy of Decision Trees (DTs) in marking OSPE questions as a potential first step to creating an intelligent, online OSPE tutoring system. The study used the results of the winter 2020 semester final OSPE from McMaster University's anatomy and physiology course in the Faculty of Health Sciences (HTHSCI 2FF3/2LL3/1D06) as the data set. Ninety percent of the data set was used in a 10-fold validation algorithm to train a DT for each of the 54 questions. Each DT was comprised of unique words that appeared in correct, student-written answers. The remaining 10% of the data set was marked by the generated DTs. When the answers marked by the DT were compared to the answers marked by staff and faculty, the DT achieved an average accuracy of 94.49% across all 54 questions. This suggests that machine learning algorithms such as DTs are a highly effective option for OSPE grading and are suitable for the development of an intelligent, online OSPE tutoring system.

Stochastic L-system Inference from Multiple String Sequence Inputs

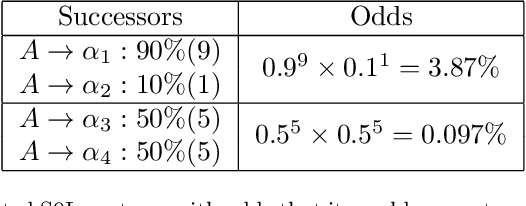
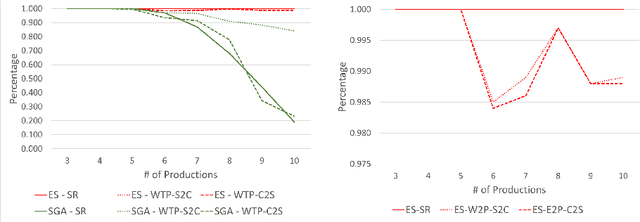
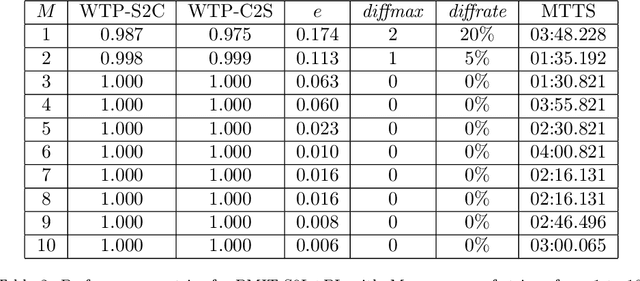
Lindenmayer systems (L-systems) are a grammar system that consist of string rewriting rules. The rules replace every symbol in a string in parallel with a successor to produce the next string, and this procedure iterates. In a stochastic context-free L-system (S0L-system), every symbol may have one or more rewriting rule, each with an associated probability of selection. Properly constructed rewriting rules have been found to be useful for modeling and simulating some natural and human engineered processes where each derived string describes a step in the simulation. Typically, processes are modeled by experts who meticulously construct the rules based on measurements or domain knowledge of the process. This paper presents an automated approach to finding stochastic L-systems, given a set of string sequences as input. The implemented tool is called the Plant Model Inference Tool for S0L-systems (PMIT-S0L). PMIT-S0L is evaluated using 960 procedurally generated S0L-systems in a test suite, which are each used to generate input strings, and PMIT-S0L is then used to infer the system from only the sequences. The evaluation shows that PMIT-S0L infers S0L-systems with up to 9 rewriting rules each in under 12 hours. Additionally, it is found that 3 sequences of strings is sufficient to find the correct original rewriting rules in 100% of the cases in the test suite, and 6 sequences of strings reduces the difference in the associated probabilities to approximately 1% or less.

New Techniques for Inferring L-Systems Using Genetic Algorithm

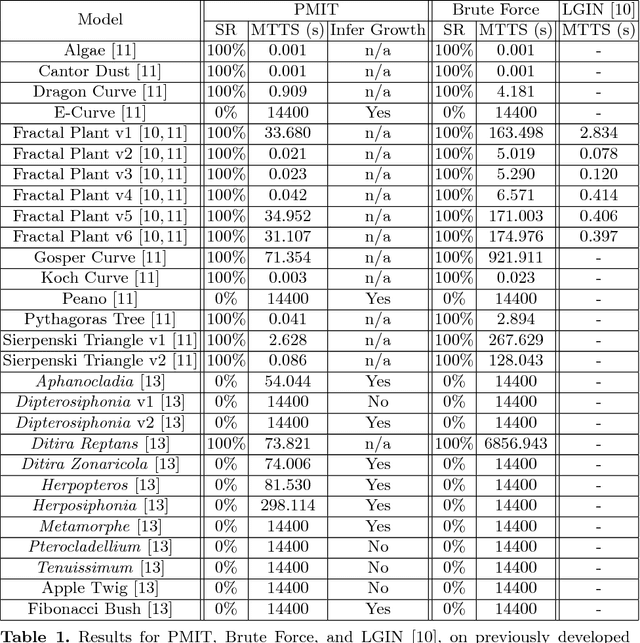
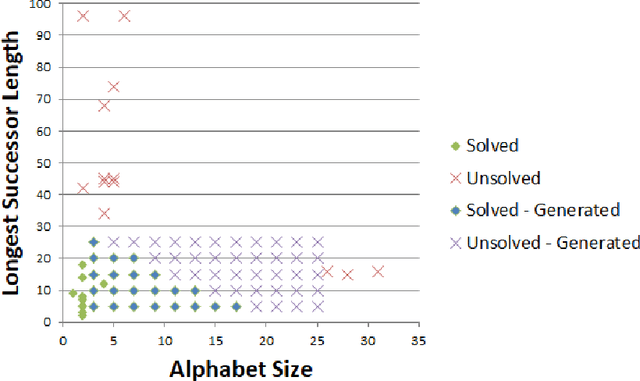
Lindenmayer systems (L-systems) are a formal grammar system that iteratively rewrites all symbols of a string, in parallel. When visualized with a graphical interpretation, the images have self-similar shapes that appear frequently in nature, and they have been particularly successful as a concise, reusable technique for simulating plants. The L-system inference problem is to find an L-system to simulate a given plant. This is currently done mainly by experts, but this process is limited by the availability of experts, the complexity that may be solved by humans, and time. This paper introduces the Plant Model Inference Tool (PMIT) that infers deterministic context-free L-systems from an initial sequence of strings generated by the system using a genetic algorithm. PMIT is able to infer more complex systems than existing approaches. Indeed, while existing approaches are limited to L-systems with a total sum of 20 combined symbols in the productions, PMIT can infer almost all L-systems tested where the total sum is 140 symbols. This was validated using a test bed of 28 previously developed L-system models, in addition to models created artificially by bootstrapping larger models.