Constraining Streaming Flow Models for Adapting Learned Robot Trajectory Distributions

Robot motion distributions often exhibit multi-modality and require flexible generative models for accurate representation. Streaming Flow Policies (SFPs) have recently emerged as a powerful paradigm for generating robot trajectories by integrating learned velocity fields directly in action space, enabling smooth and reactive control. However, existing formulations lack mechanisms for adapting trajectories post-training to enforce safety and task-specific constraints. We propose Constraint-Aware Streaming Flow (CASF), a framework that augments streaming flow policies with constraint-dependent metrics that reshape the learned velocity field during execution. CASF models each constraint, defined in either the robot's workspace or configuration space, as a differentiable distance function that is converted into a local metric and pulled back into the robot's control space. Far from restricted regions, the resulting metric reduces to the identity; near constraint boundaries, it smoothly attenuates or redirects motion, effectively deforming the underlying flow to maintain safety. This allows trajectories to be adapted in real time, ensuring that robot actions respect joint limits, avoid collisions, and remain within feasible workspaces, while preserving the multi-modal and reactive properties of streaming flow policies. We demonstrate CASF in simulated and real-world manipulation tasks, showing that it produces constraint-satisfying trajectories that remain smooth, feasible, and dynamically consistent, outperforming standard post-hoc projection baselines.

LipKernel: Lipschitz-Bounded Convolutional Neural Networks via Dissipative Layers

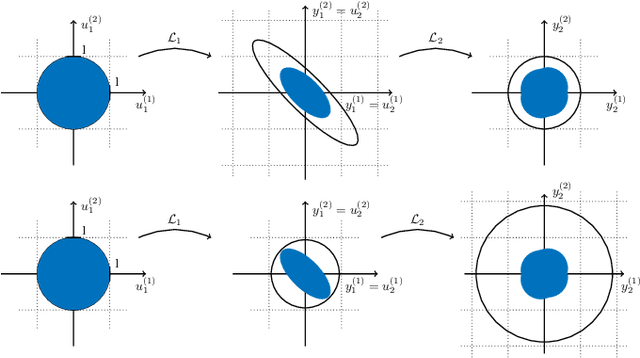
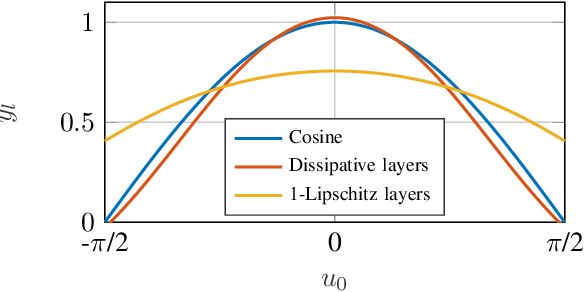
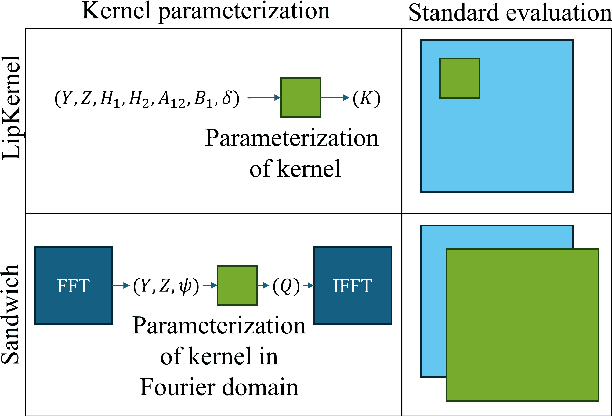
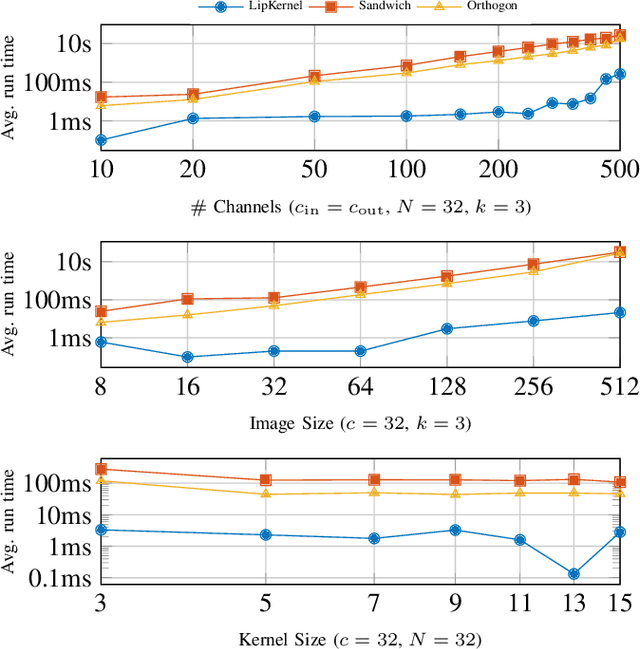
We propose a novel layer-wise parameterization for convolutional neural networks (CNNs) that includes built-in robustness guarantees by enforcing a prescribed Lipschitz bound. Each layer in our parameterization is designed to satisfy a linear matrix inequality (LMI), which in turn implies dissipativity with respect to a specific supply rate. Collectively, these layer-wise LMIs ensure Lipschitz boundedness for the input-output mapping of the neural network, yielding a more expressive parameterization than through spectral bounds or orthogonal layers. Our new method LipKernel directly parameterizes dissipative convolution kernels using a 2-D Roesser-type state space model. This means that the convolutional layers are given in standard form after training and can be evaluated without computational overhead. In numerical experiments, we show that the run-time using our method is orders of magnitude faster than state-of-the-art Lipschitz-bounded networks that parameterize convolutions in the Fourier domain, making our approach particularly attractive for improving robustness of learning-based real-time perception or control in robotics, autonomous vehicles, or automation systems. We focus on CNNs, and in contrast to previous works, our approach accommodates a wide variety of layers typically used in CNNs, including 1-D and 2-D convolutional layers, maximum and average pooling layers, as well as strided and dilated convolutions and zero padding. However, our approach naturally extends beyond CNNs as we can incorporate any layer that is incrementally dissipative.