LipKernel: Lipschitz-Bounded Convolutional Neural Networks via Dissipative Layers
Paper and Code
Oct 29, 2024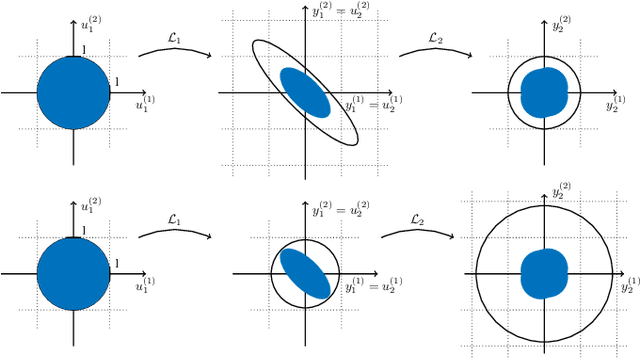
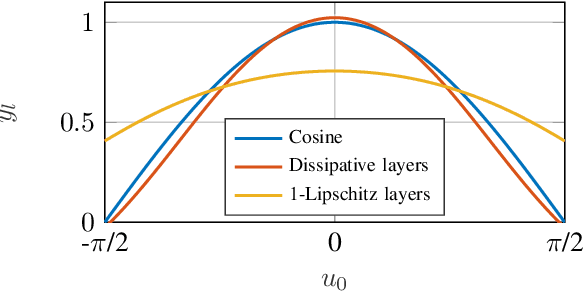
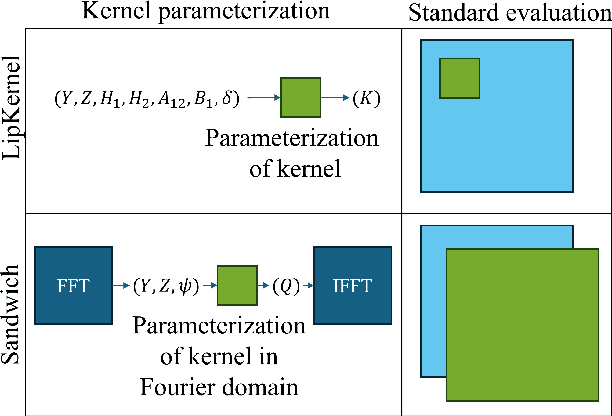
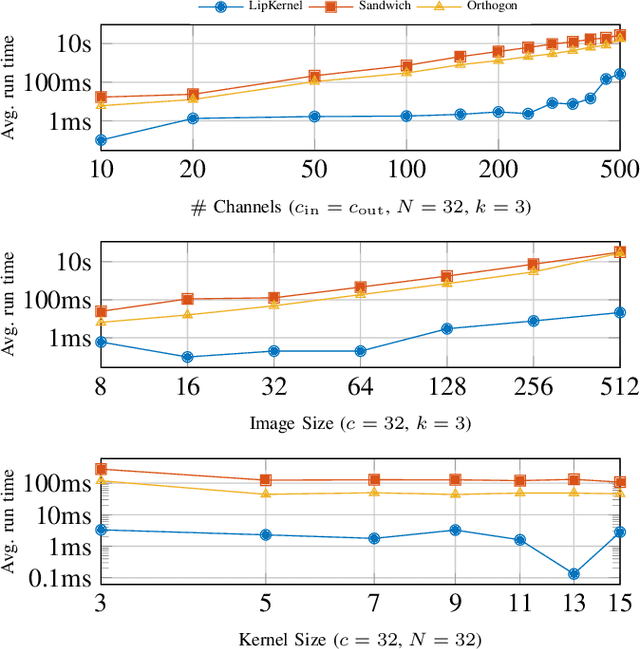
We propose a novel layer-wise parameterization for convolutional neural networks (CNNs) that includes built-in robustness guarantees by enforcing a prescribed Lipschitz bound. Each layer in our parameterization is designed to satisfy a linear matrix inequality (LMI), which in turn implies dissipativity with respect to a specific supply rate. Collectively, these layer-wise LMIs ensure Lipschitz boundedness for the input-output mapping of the neural network, yielding a more expressive parameterization than through spectral bounds or orthogonal layers. Our new method LipKernel directly parameterizes dissipative convolution kernels using a 2-D Roesser-type state space model. This means that the convolutional layers are given in standard form after training and can be evaluated without computational overhead. In numerical experiments, we show that the run-time using our method is orders of magnitude faster than state-of-the-art Lipschitz-bounded networks that parameterize convolutions in the Fourier domain, making our approach particularly attractive for improving robustness of learning-based real-time perception or control in robotics, autonomous vehicles, or automation systems. We focus on CNNs, and in contrast to previous works, our approach accommodates a wide variety of layers typically used in CNNs, including 1-D and 2-D convolutional layers, maximum and average pooling layers, as well as strided and dilated convolutions and zero padding. However, our approach naturally extends beyond CNNs as we can incorporate any layer that is incrementally dissipative.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge