Optimal Architecture for Deep Neural Networks with Heterogeneous Sensitivity

This work presents a neural network that consists of nodes with heterogeneous sensitivity. Each node in a network is assigned a variable that determines the sensitivity with which it learns to perform a given task. The network is trained by a constrained optimization that minimizes the sparsity of the sensitivity variables while ensuring the network's performance. As a result, the network learns to perform a given task using only a small number of sensitive nodes. The L-curve is used to find a regularization parameter for the constrained optimization. To validate our approach, we design networks with optimal architectures for autoregression, object recognition, facial expression recognition, and object detection. In our experiments, the optimal networks designed by the proposed method provide the same or higher performance but with far less computational complexity.

Deep Asymmetric Networks with a Set of Node-wise Variant Activation Functions

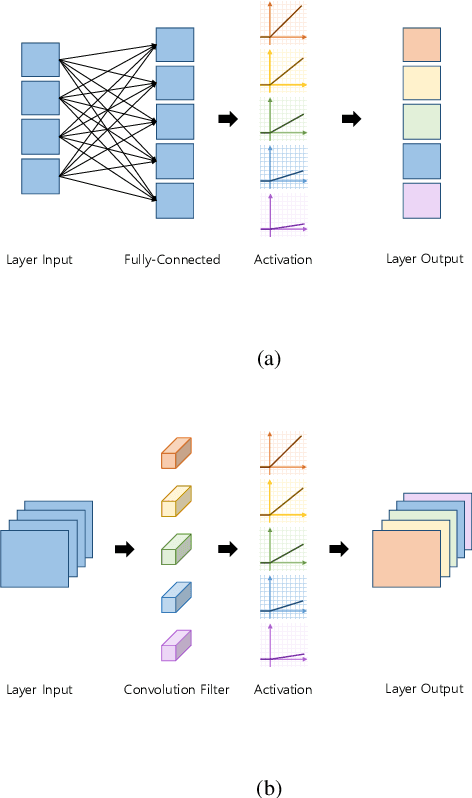
This work presents deep asymmetric networks with a set of node-wise variant activation functions. The nodes' sensitivities are affected by activation function selections such that the nodes with smaller indices become increasingly more sensitive. As a result, features learned by the nodes are sorted by the node indices in the order of their importance. Asymmetric networks not only learn input features but also the importance of those features. Nodes of lesser importance in asymmetric networks can be pruned to reduce the complexity of the networks, and the pruned networks can be retrained without incurring performance losses. We validate the feature-sorting property using both shallow and deep asymmetric networks as well as deep asymmetric networks transferred from famous networks.