Discrete Dictionary-based Decomposition Layer for Structured Representation Learning

Neuro-symbolic neural networks have been extensively studied to integrate symbolic operations with neural networks, thereby improving systematic generalization. Specifically, Tensor Product Representation (TPR) framework enables neural networks to perform differentiable symbolic operations by encoding the symbolic structure of data within vector spaces. However, TPR-based neural networks often struggle to decompose unseen data into structured TPR representations, undermining their symbolic operations. To address this decomposition problem, we propose a Discrete Dictionary-based Decomposition (D3) layer designed to enhance the decomposition capabilities of TPR-based models. D3 employs discrete, learnable key-value dictionaries trained to capture symbolic features essential for decomposition operations. It leverages the prior knowledge acquired during training to generate structured TPR representations by mapping input data to pre-learned symbolic features within these dictionaries. D3 is a straightforward drop-in layer that can be seamlessly integrated into any TPR-based model without modifications. Our experimental results demonstrate that D3 significantly improves the systematic generalization of various TPR-based models while requiring fewer additional parameters. Notably, D3 outperforms baseline models on the synthetic task that demands the systematic decomposition of unseen combinatorial data.

Bayesian Model Selection Methods for Mutual and Symmetric $k$-Nearest Neighbor Classification

The $k$-nearest neighbor classification method ($k$-NNC) is one of the simplest nonparametric classification methods. The mutual $k$-NN classification method (M$k$NNC) is a variant of $k$-NNC based on mutual neighborship. We propose another variant of $k$-NNC, the symmetric $k$-NN classification method (S$k$NNC) based on both mutual neighborship and one-sided neighborship. The performance of M$k$NNC and S$k$NNC depends on the parameter $k$ as the one of $k$-NNC does. We propose the ways how M$k$NN and S$k$NN classification can be performed based on Bayesian mutual and symmetric $k$-NN regression methods with the selection schemes for the parameter $k$. Bayesian mutual and symmetric $k$-NN regression methods are based on Gaussian process models, and it turns out that they can do M$k$NN and S$k$NN classification with new encodings of target values (class labels). The simulation results show that the proposed methods are better than or comparable to $k$-NNC, M$k$NNC and S$k$NNC with the parameter $k$ selected by the leave-one-out cross validation method not only for an artificial data set but also for real world data sets.

Bayesian Kernel and Mutual $k$-Nearest Neighbor Regression

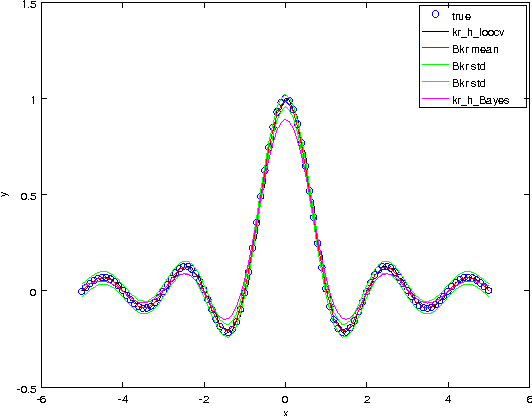
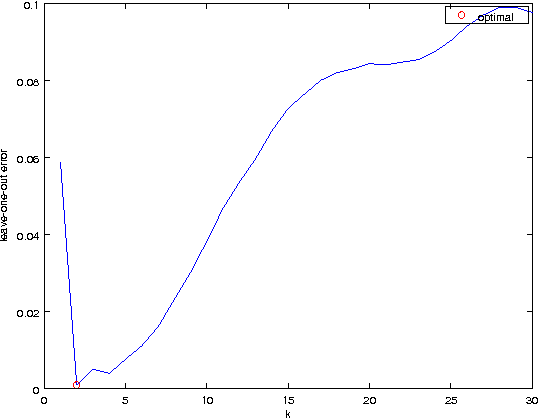
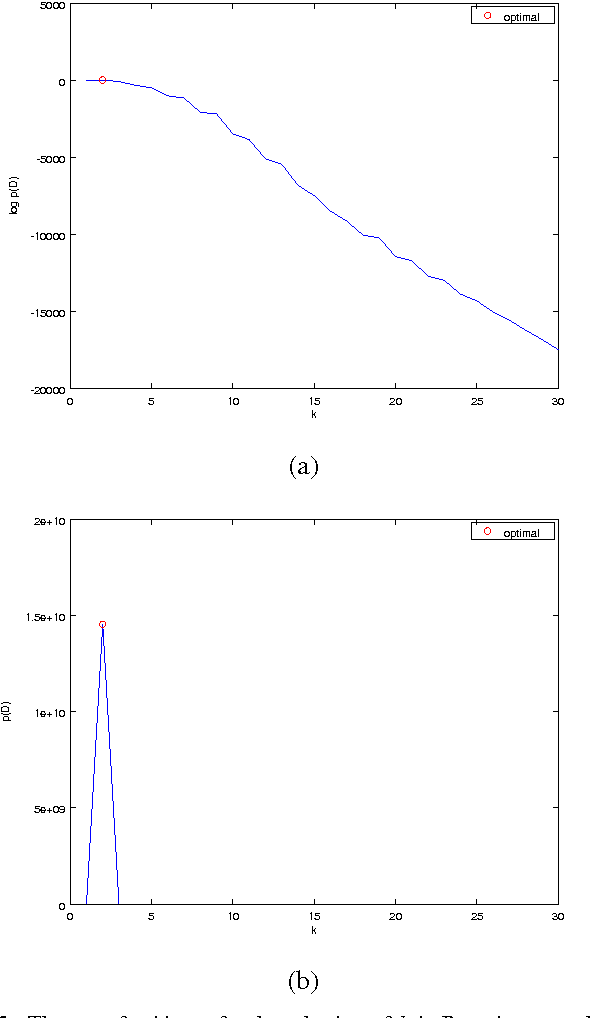
We propose Bayesian extensions of two nonparametric regression methods which are kernel and mutual $k$-nearest neighbor regression methods. Derived based on Gaussian process models for regression, the extensions provide distributions for target value estimates and the framework to select the hyperparameters. It is shown that both the proposed methods asymptotically converge to kernel and mutual $k$-nearest neighbor regression methods, respectively. The simulation results show that the proposed methods can select proper hyperparameters and are better than or comparable to the former methods for an artificial data set and a real world data set.