Bayesian Kernel and Mutual $k$-Nearest Neighbor Regression
Paper and Code
Aug 04, 2016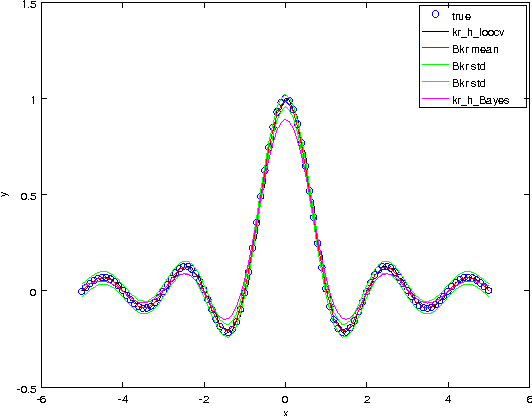

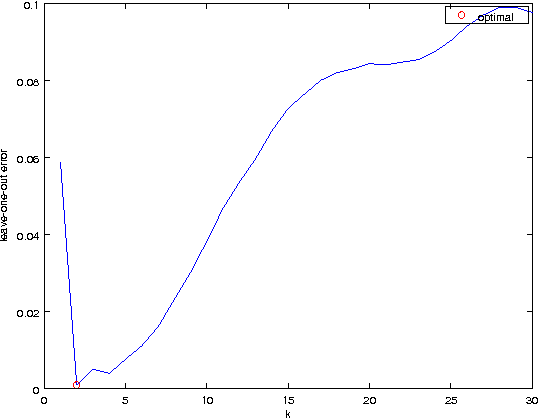
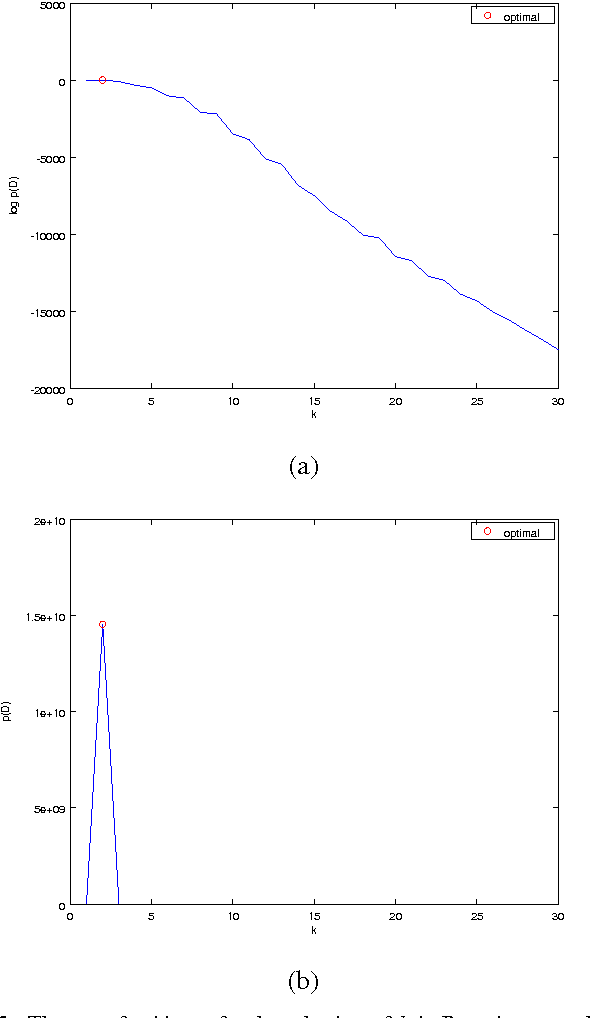
We propose Bayesian extensions of two nonparametric regression methods which are kernel and mutual $k$-nearest neighbor regression methods. Derived based on Gaussian process models for regression, the extensions provide distributions for target value estimates and the framework to select the hyperparameters. It is shown that both the proposed methods asymptotically converge to kernel and mutual $k$-nearest neighbor regression methods, respectively. The simulation results show that the proposed methods can select proper hyperparameters and are better than or comparable to the former methods for an artificial data set and a real world data set.
* 8 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge