An extended asymmetric sigmoid with Perceptron (SIGTRON) for imbalanced linear classification

This article presents a new polynomial parameterized sigmoid called SIGTRON, which is an extended asymmetric sigmoid with Perceptron, and its companion convex model called SIGTRON-imbalanced classification (SIC) model that employs a virtual SIGTRON-induced convex loss function. In contrast to the conventional $\pi$-weighted cost-sensitive learning model, the SIC model does not have an external $\pi$-weight on the loss function but has internal parameters in the virtual SIGTRON-induced loss function. As a consequence, when the given training dataset is close to the well-balanced condition, we show that the proposed SIC model is more adaptive to variations of the dataset, such as the inconsistency of the scale-class-imbalance ratio between the training and test datasets. This adaptation is achieved by creating a skewed hyperplane equation. Additionally, we present a quasi-Newton optimization(L-BFGS) framework for the virtual convex loss by developing an interval-based bisection line search. Empirically, we have observed that the proposed approach outperforms $\pi$-weighted convex focal loss and balanced classifier LIBLINEAR(logistic regression, SVM, and L2SVM) in terms of test classification accuracy with $51$ two-class and $67$ multi-class datasets. In binary classification problems, where the scale-class-imbalance ratio of the training dataset is not significant but the inconsistency exists, a group of SIC models with the best test accuracy for each dataset (TOP$1$) outperforms LIBSVM(C-SVC with RBF kernel), a well-known kernel-based classifier.

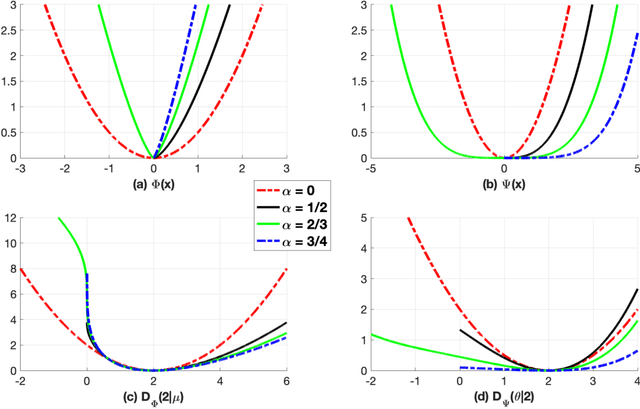
Bregman-divergence-guided Legendre exponential dispersion model with finite cumulants (K-LED)

Exponential dispersion model is a useful framework in machine learning and statistics. Primarily, thanks to the additive structure of the model, it can be achieved without difficulty to estimate parameters including mean. However, tight conditions on cumulant function, such as analyticity, strict convexity, and steepness, reduce the class of exponential dispersion model. In this work, we present relaxed exponential dispersion model K-LED (Legendre exponential dispersion model with K cumulants). The cumulant function of the proposed model is a convex function of Legendre type having continuous partial derivatives of K-th order on the interior of a convex domain. Most of the K-LED models are developed via Bregman-divergence-guided log-concave density function with coercivity shape constraints. The main advantage of the proposed model is that the first cumulant (or the mean parameter space) of the 1-LED model is easily computed through the extended global optimum property of Bregman divergence. An extended normal distribution is introduced as an example of 1-LED based on Tweedie distribution. On top of that, we present 2-LED satisfying mean-variance relation of quasi-likelihood function. There is an equivalence between a subclass of quasi-likelihood function and a regular 2-LED model, of which the canonical parameter space is open. A typical example is a regular 2-LED model with power variance function, i.e., a variance is in proportion to the power of the mean of observations. This model is equivalent to a subclass of beta-divergence (or a subclass of quasi-likelihood function with power variance function). Furthermore, a new parameterized K-LED model, the cumulant function of which is the convex extended logistic loss function, is proposed. This model includes Bernoulli distribution and Poisson distribution.

The Bregman-Tweedie Classification Model

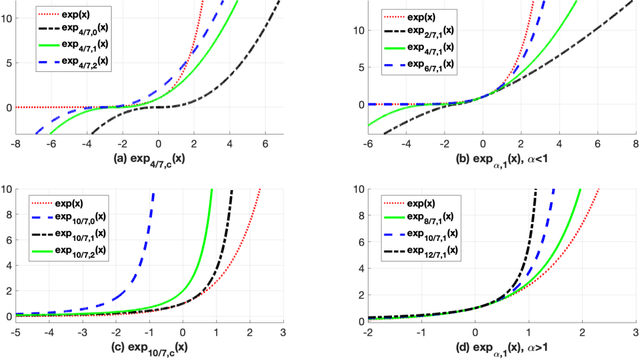
This work proposes the Bregman-Tweedie classification model and analyzes the domain structure of the extended exponential function, an extension of the classic generalized exponential function with additional scaling parameter, and related high-level mathematical structures, such as the Bregman-Tweedie loss function and the Bregman-Tweedie divergence. The base function of this divergence is the convex function of Legendre type induced from the extended exponential function. The Bregman-Tweedie loss function of the proposed classification model is the regular Legendre transformation of the Bregman-Tweedie divergence. This loss function is a polynomial parameterized function between unhinge loss and the logistic loss function. Actually, we have two sub-models of the Bregman-Tweedie classification model; H-Bregman with hinge-like loss function and L-Bregman with logistic-like loss function. Although the proposed classification model is nonconvex and unbounded, empirically, we have observed that the H-Bregman and L-Bregman outperform, in terms of the Friedman ranking, logistic regression and SVM and show reasonable performance in terms of the classification accuracy in the category of the binary linear classification problem.

Logitron: Perceptron-augmented classification model based on an extended logistic loss function

Classification is the most important process in data analysis. However, due to the inherent non-convex and non-smooth structure of the zero-one loss function of the classification model, various convex surrogate loss functions such as hinge loss, squared hinge loss, logistic loss, and exponential loss are introduced. These loss functions have been used for decades in diverse classification models, such as SVM (support vector machine) with hinge loss, logistic regression with logistic loss, and Adaboost with exponential loss and so on. In this work, we present a Perceptron-augmented convex classification framework, {\it Logitron}. The loss function of it is a smoothly stitched function of the extended logistic loss with the famous Perceptron loss function. The extended logistic loss function is a parameterized function established based on the extended logarithmic function and the extended exponential function. The main advantage of the proposed Logitron classification model is that it shows the connection between SVM and logistic regression via polynomial parameterization of the loss function. In more details, depending on the choice of parameters, we have the Hinge-Logitron which has the generalized $k$-th order hinge-loss with an additional $k$-th root stabilization function and the Logistic-Logitron which has a logistic-like loss function with relatively large $|k|$. Interestingly, even $k=-1$, Hinge-Logitron satisfies the classification-calibration condition and shows reasonable classification performance with low computational cost. The numerical experiment in the linear classifier framework demonstrates that Hinge-Logitron with $k=4$ (the fourth-order SVM with the fourth root stabilization function) outperforms logistic regression, SVM, and other Logitron models in terms of classification accuracy.

Outlier Detection for Text Data : An Extended Version

The problem of outlier detection is extremely challenging in many domains such as text, in which the attribute values are typically non-negative, and most values are zero. In such cases, it often becomes difficult to separate the outliers from the natural variations in the patterns in the underlying data. In this paper, we present a matrix factorization method, which is naturally able to distinguish the anomalies with the use of low rank approximations of the underlying data. Our iterative algorithm TONMF is based on block coordinate descent (BCD) framework. We define blocks over the term-document matrix such that the function becomes solvable. Given most recently updated values of other matrix blocks, we always update one block at a time to its optimal. Our approach has significant advantages over traditional methods for text outlier detection. Finally, we present experimental results illustrating the effectiveness of our method over competing methods.