The Bregman-Tweedie Classification Model
Paper and Code
Jul 16, 2019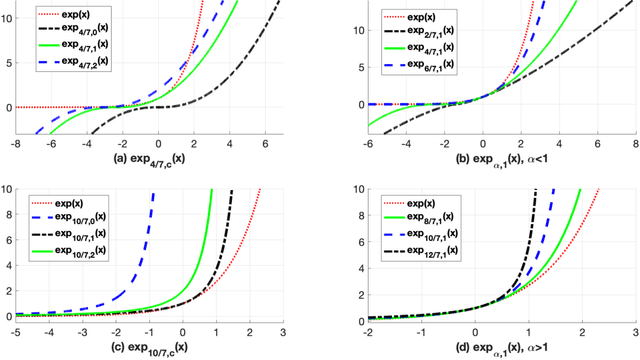


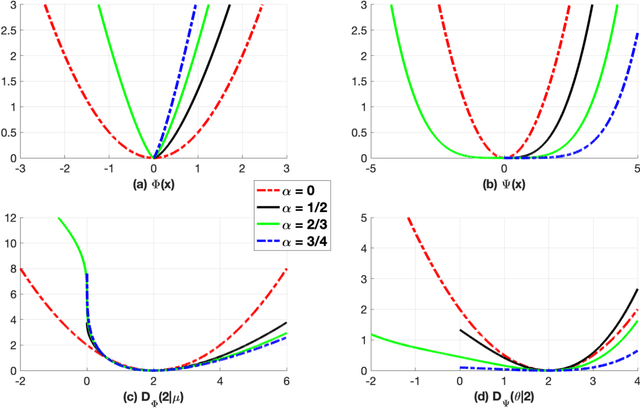
This work proposes the Bregman-Tweedie classification model and analyzes the domain structure of the extended exponential function, an extension of the classic generalized exponential function with additional scaling parameter, and related high-level mathematical structures, such as the Bregman-Tweedie loss function and the Bregman-Tweedie divergence. The base function of this divergence is the convex function of Legendre type induced from the extended exponential function. The Bregman-Tweedie loss function of the proposed classification model is the regular Legendre transformation of the Bregman-Tweedie divergence. This loss function is a polynomial parameterized function between unhinge loss and the logistic loss function. Actually, we have two sub-models of the Bregman-Tweedie classification model; H-Bregman with hinge-like loss function and L-Bregman with logistic-like loss function. Although the proposed classification model is nonconvex and unbounded, empirically, we have observed that the H-Bregman and L-Bregman outperform, in terms of the Friedman ranking, logistic regression and SVM and show reasonable performance in terms of the classification accuracy in the category of the binary linear classification problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge