A Direct Estimation of High Dimensional Stationary Vector Autoregressions

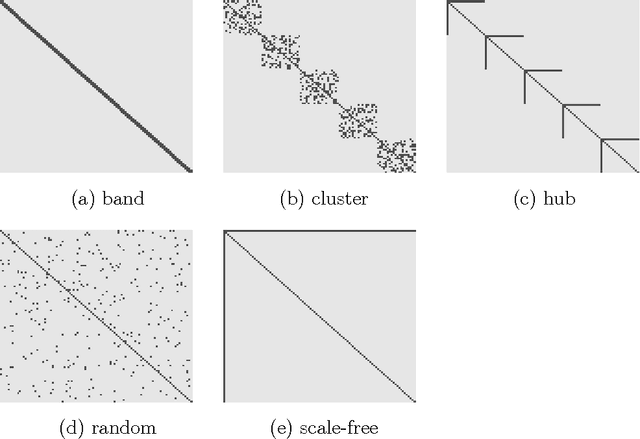
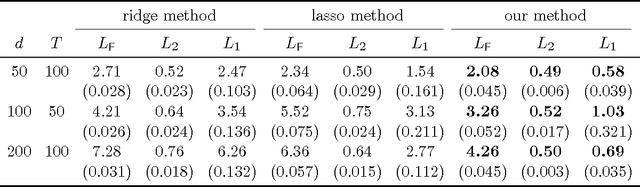
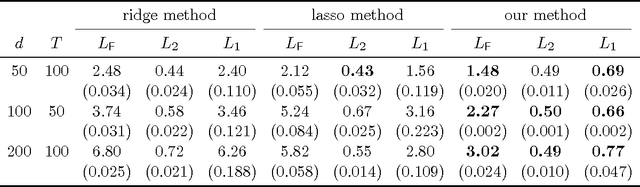
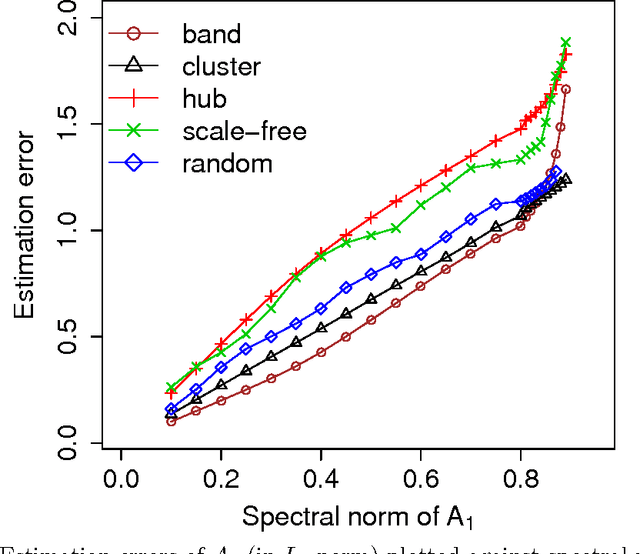
The vector autoregressive (VAR) model is a powerful tool in modeling complex time series and has been exploited in many fields. However, fitting high dimensional VAR model poses some unique challenges: On one hand, the dimensionality, caused by modeling a large number of time series and higher order autoregressive processes, is usually much higher than the time series length; On the other hand, the temporal dependence structure in the VAR model gives rise to extra theoretical challenges. In high dimensions, one popular approach is to assume the transition matrix is sparse and fit the VAR model using the "least squares" method with a lasso-type penalty. In this manuscript, we propose an alternative way in estimating the VAR model. The main idea is, via exploiting the temporal dependence structure, to formulate the estimating problem into a linear program. There is instant advantage for the proposed approach over the lasso-type estimators: The estimation equation can be decomposed into multiple sub-equations and accordingly can be efficiently solved in a parallel fashion. In addition, our method brings new theoretical insights into the VAR model analysis. So far the theoretical results developed in high dimensions (e.g., Song and Bickel (2011) and Kock and Callot (2012)) mainly pose assumptions on the design matrix of the formulated regression problems. Such conditions are indirect about the transition matrices and not transparent. In contrast, our results show that the operator norm of the transition matrices plays an important role in estimation accuracy. We provide explicit rates of convergence for both estimation and prediction. In addition, we provide thorough experiments on both synthetic and real-world equity data to show that there are empirical advantages of our method over the lasso-type estimators in both parameter estimation and forecasting.

Nonconvex Statistical Optimization: Minimax-Optimal Sparse PCA in Polynomial Time

Sparse principal component analysis (PCA) involves nonconvex optimization for which the global solution is hard to obtain. To address this issue, one popular approach is convex relaxation. However, such an approach may produce suboptimal estimators due to the relaxation effect. To optimally estimate sparse principal subspaces, we propose a two-stage computational framework named "tighten after relax": Within the 'relax' stage, we approximately solve a convex relaxation of sparse PCA with early stopping to obtain a desired initial estimator; For the 'tighten' stage, we propose a novel algorithm called sparse orthogonal iteration pursuit (SOAP), which iteratively refines the initial estimator by directly solving the underlying nonconvex problem. A key concept of this two-stage framework is the basin of attraction. It represents a local region within which the `tighten' stage has desired computational and statistical guarantees. We prove that, the initial estimator obtained from the 'relax' stage falls into such a region, and hence SOAP geometrically converges to a principal subspace estimator which is minimax-optimal within a certain model class. Unlike most existing sparse PCA estimators, our approach applies to the non-spiked covariance models, and adapts to non-Gaussianity as well as dependent data settings. Moreover, through analyzing the computational complexity of the two stages, we illustrate an interesting phenomenon that larger sample size can reduce the total iteration complexity. Our framework motivates a general paradigm for solving many complex statistical problems which involve nonconvex optimization with provable guarantees.