A Systematic Reproducibility Study of BSARec for Sequential Recommendation

In sequential recommendation (SR), the self-attention mechanism of Transformer-based models acts as a low-pass filter, limiting their ability to capture high-frequency signals that reflect short-term user interests. To overcome this, BSARec augments the Transformer encoder with a frequency layer that rescales high-frequency components using the Fourier transform. However, the overall effectiveness of BSARec and the roles of its individual components have yet to be systematically validated. We reproduce BSARec and show that it outperforms other SR methods on some datasets. To empirically assess whether BSARec improves performance on high-frequency signals, we propose a metric to quantify user history frequency and evaluate SR methods across different user groups. We compare digital signal processing (DSP) techniques and find that the discrete wavelet transform (DWT) offer only slight improvements over Fourier transforms, and DSP methods provide no clear advantage over simple residual connections. Finally, we explore padding strategies and find that non-constant padding significantly improves recommendation performance, whereas constant padding hinders the frequency rescaler's ability to capture high-frequency signals.

Keep your distance: learning dispersed embeddings on $\mathbb{S}_d$

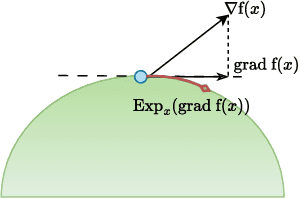
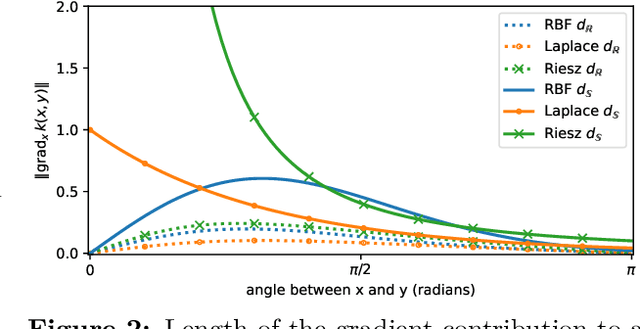
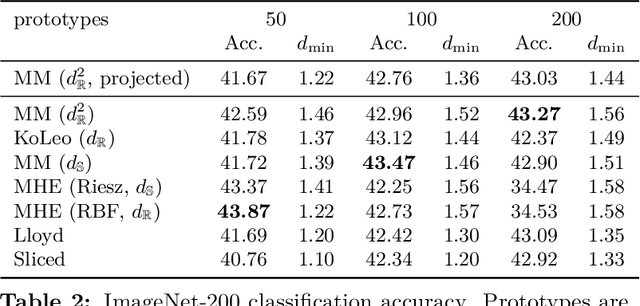
Learning well-separated features in high-dimensional spaces, such as text or image embeddings, is crucial for many machine learning applications. Achieving such separation can be effectively accomplished through the dispersion of embeddings, where unrelated vectors are pushed apart as much as possible. By constraining features to be on a hypersphere, we can connect dispersion to well-studied problems in mathematics and physics, where optimal solutions are known for limited low-dimensional cases. However, in representation learning we typically deal with a large number of features in high-dimensional space, and moreover, dispersion is usually traded off with some other task-oriented training objective, making existing theoretical and numerical solutions inapplicable. Therefore, it is common to rely on gradient-based methods to encourage dispersion, usually by minimizing some function of the pairwise distances. In this work, we first give an overview of existing methods from disconnected literature, making new connections and highlighting similarities. Next, we introduce some new angles. We propose to reinterpret pairwise dispersion using a maximum mean discrepancy (MMD) motivation. We then propose an online variant of the celebrated Lloyd's algorithm, of K-Means fame, as an effective alternative regularizer for dispersion on generic domains. Finally, we derive a novel dispersion method that directly exploits properties of the hypersphere. Our experiments show the importance of dispersion in image classification and natural language processing tasks, and how algorithms exhibit different trade-offs in different regimes.

A Simpler Alternative to Variational Regularized Counterfactual Risk Minimization

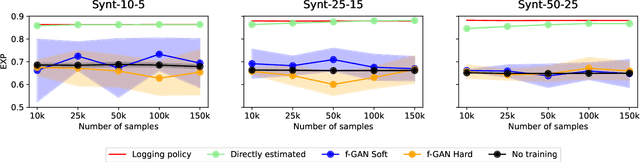
Variance regularized counterfactual risk minimization (VRCRM) has been proposed as an alternative off-policy learning (OPL) method. VRCRM method uses a lower-bound on the $f$-divergence between the logging policy and the target policy as regularization during learning and was shown to improve performance over existing OPL alternatives on multi-label classification tasks. In this work, we revisit the original experimental setting of VRCRM and propose to minimize the $f$-divergence directly, instead of optimizing for the lower bound using a $f$-GAN approach. Surprisingly, we were unable to reproduce the results reported in the original setting. In response, we propose a novel simpler alternative to f-divergence optimization by minimizing a direct approximation of f-divergence directly, instead of a $f$-GAN based lower bound. Experiments showed that minimizing the divergence using $f$-GANs did not work as expected, whereas our proposed novel simpler alternative works better empirically.