Hristos Tyralis
Transformations of predictions and realizations in consistent scoring functions
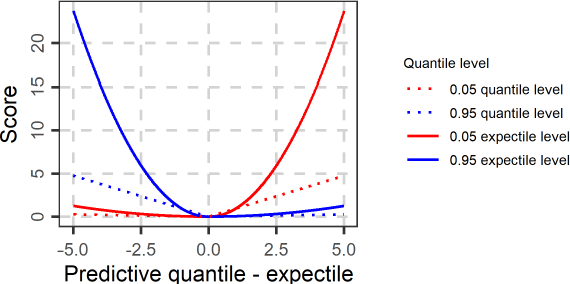
Feb 23, 2025Abstract:Scoring functions constructed by transforming the realization and prediction variables of (strictly) consistent scoring functions have been widely studied empirically, yet their theoretical foundations remain unexplored. To address this gap, we establish formal characterizations of (strict) consistency for these transformed scoring functions and their elicitable functionals. Our analysis focuses on two interrelated cases: (a) transformations applied exclusively to the realization variable, and (b) bijective transformations applied jointly to both realization and prediction variables. We formulate analogous characterizations for (strict) identification functions. The resulting theoretical framework is broadly applicable to statistical and machine learning methodologies. When applied to Bregman and expectile scoring functions, our framework shows how it enables two critical advances: (a) rigorous interpretation of prior empirical findings from models trained with transformed scoring functions, and (b) systematic construction of novel identifiable and elicitable functionals, specifically the g-transformed expectation and g-transformed expectile. By unifying theoretical insights with practical applications, this work advances principled methodologies for designing scoring functions in complex predictive tasks.
Uncertainty estimation in satellite precipitation spatial prediction by combining distributional regression algorithms
Jun 29, 2024Abstract:To facilitate effective decision-making, gridded satellite precipitation products should include uncertainty estimates. Machine learning has been proposed for issuing such estimates. However, most existing algorithms for this purpose rely on quantile regression. Distributional regression offers distinct advantages over quantile regression, including the ability to model intermittency as well as a stronger ability to extrapolate beyond the training data, which is critical for predicting extreme precipitation. In this work, we introduce the concept of distributional regression for the engineering task of creating precipitation datasets through data merging. Building upon this concept, we propose new ensemble learning methods that can be valuable not only for spatial prediction but also for prediction problems in general. These methods exploit conditional zero-adjusted probability distributions estimated with generalized additive models for location, scale, and shape (GAMLSS), spline-based GAMLSS and distributional regression forests as well as their ensembles (stacking based on quantile regression, and equal-weight averaging). To identify the most effective methods for our specific problem, we compared them to benchmarks using a large, multi-source precipitation dataset. Stacking emerged as the most successful strategy. Three specific stacking methods achieved the best performance based on the quantile scoring rule, although the ranking of these methods varied across quantile levels. This suggests that a task-specific combination of multiple algorithms could yield significant benefits.
Uncertainty estimation in spatial interpolation of satellite precipitation with ensemble learning
Mar 14, 2024Abstract:Predictions in the form of probability distributions are crucial for decision-making. Quantile regression enables this within spatial interpolation settings for merging remote sensing and gauge precipitation data. However, ensemble learning of quantile regression algorithms remains unexplored in this context. Here, we address this gap by introducing nine quantile-based ensemble learners and applying them to large precipitation datasets. We employed a novel feature engineering strategy, reducing predictors to distance-weighted satellite precipitation at relevant locations, combined with location elevation. Our ensemble learners include six stacking and three simple methods (mean, median, best combiner), combining six individual algorithms: quantile regression (QR), quantile regression forests (QRF), generalized random forests (GRF), gradient boosting machines (GBM), light gradient boosting machines (LightGBM), and quantile regression neural networks (QRNN). These algorithms serve as both base learners and combiners within different stacking methods. We evaluated performance against QR using quantile scoring functions in a large dataset comprising 15 years of monthly gauge-measured and satellite precipitation in contiguous US (CONUS). Stacking with QR and QRNN yielded the best results across quantile levels of interest (0.025, 0.050, 0.075, 0.100, 0.200, 0.300, 0.400, 0.500, 0.600, 0.700, 0.800, 0.900, 0.925, 0.950, 0.975), surpassing the reference method by 3.91% to 8.95%. This demonstrates the potential of stacking to improve probabilistic predictions in spatial interpolation and beyond.
Machine learning for uncertainty estimation in fusing precipitation observations from satellites and ground-based gauges
Nov 13, 2023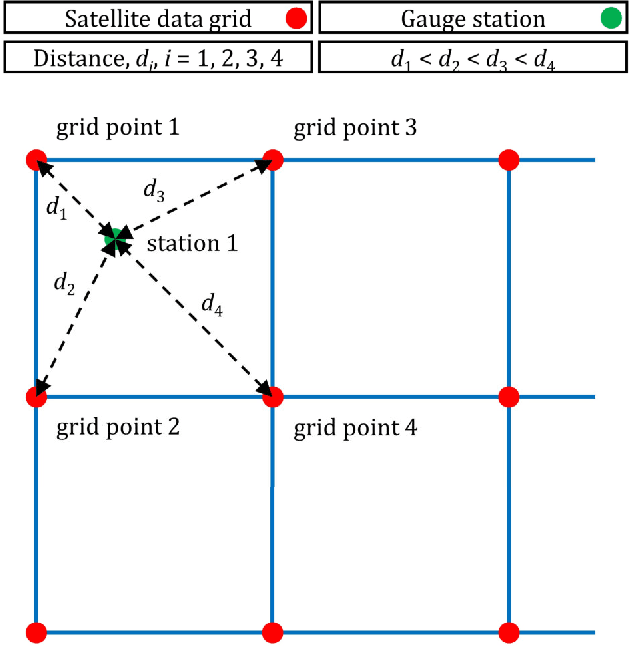
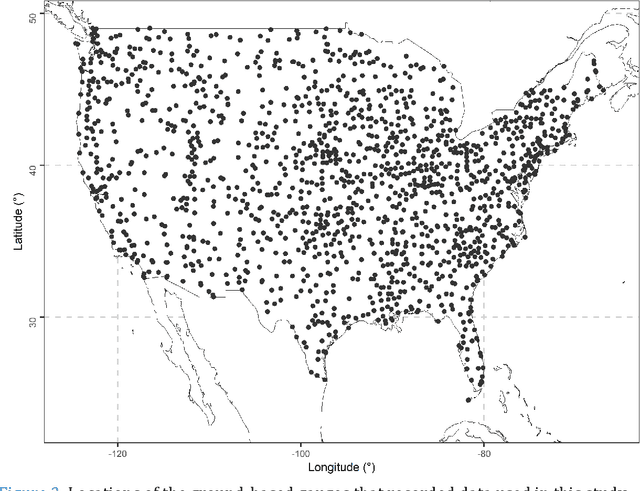
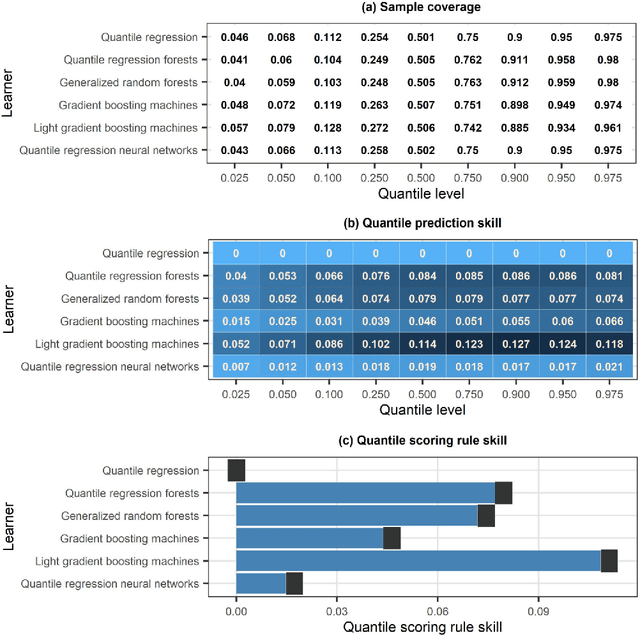

Abstract:To form precipitation datasets that are accurate and, at the same time, have high spatial densities, data from satellites and gauges are often merged in the literature. However, uncertainty estimates for the data acquired in this manner are scarcely provided, although the importance of uncertainty quantification in predictive modelling is widely recognized. Furthermore, the benefits that machine learning can bring to the task of providing such estimates have not been broadly realized and properly explored through benchmark experiments. The present study aims at filling in this specific gap by conducting the first benchmark tests on the topic. On a large dataset that comprises 15-year-long monthly data spanning across the contiguous United States, we extensively compared six learners that are, by their construction, appropriate for predictive uncertainty quantification. These are the quantile regression (QR), quantile regression forests (QRF), generalized random forests (GRF), gradient boosting machines (GBM), light gradient boosting machines (LightGBM) and quantile regression neural networks (QRNN). The comparison referred to the competence of the learners in issuing predictive quantiles at nine levels that facilitate a good approximation of the entire predictive probability distribution, and was primarily based on the quantile and continuous ranked probability skill scores. Three types of predictor variables (i.e., satellite precipitation variables, distances between a point of interest and satellite grid points, and elevation at a point of interest) were used in the comparison and were additionally compared with each other. This additional comparison was based on the explainable machine learning concept of feature importance. The results suggest that the order from the best to the worst of the learners for the task investigated is the following: LightGBM, QRF, GRF, GBM, QRNN and QR...
Ensemble learning for blending gridded satellite and gauge-measured precipitation data
Jul 09, 2023Abstract:Regression algorithms are regularly used for improving the accuracy of satellite precipitation products. In this context, ground-based measurements are the dependent variable and the satellite data are the predictor variables, together with topography factors. Alongside this, it is increasingly recognised in many fields that combinations of algorithms through ensemble learning can lead to substantial predictive performance improvements. Still, a sufficient number of ensemble learners for improving the accuracy of satellite precipitation products and their large-scale comparison are currently missing from the literature. In this work, we fill this specific gap by proposing 11 new ensemble learners in the field and by extensively comparing them for the entire contiguous United States and for a 15-year period. We use monthly data from the PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) and IMERG (Integrated Multi-satellitE Retrievals for GPM) gridded datasets. We also use gauge-measured precipitation data from the Global Historical Climatology Network monthly database, version 2 (GHCNm). The ensemble learners combine the predictions by six regression algorithms (base learners), namely the multivariate adaptive regression splines (MARS), multivariate adaptive polynomial splines (poly-MARS), random forests (RF), gradient boosting machines (GBM), extreme gradient boosting (XGBoost) and Bayesian regularized neural networks (BRNN), and each of them is based on a different combiner. The combiners include the equal-weight combiner, the median combiner, two best learners and seven variants of a sophisticated stacking method. The latter stacks a regression algorithm on the top of the base learners to combine their independent predictions...
Deep Huber quantile regression networks
Jun 17, 2023Abstract:Typical machine learning regression applications aim to report the mean or the median of the predictive probability distribution, via training with a squared or an absolute error scoring function. The importance of issuing predictions of more functionals of the predictive probability distribution (quantiles and expectiles) has been recognized as a means to quantify the uncertainty of the prediction. In deep learning (DL) applications, that is possible through quantile and expectile regression neural networks (QRNN and ERNN respectively). Here we introduce deep Huber quantile regression networks (DHQRN) that nest QRNNs and ERNNs as edge cases. DHQRN can predict Huber quantiles, which are more general functionals in the sense that they nest quantiles and expectiles as limiting cases. The main idea is to train a deep learning algorithm with the Huber quantile regression function, which is consistent for the Huber quantile functional. As a proof of concept, DHQRN are applied to predict house prices in Australia. In this context, predictive performances of three DL architectures are discussed along with evidential interpretation of results from an economic case study.
Merging satellite and gauge-measured precipitation using LightGBM with an emphasis on extreme quantiles
Feb 02, 2023Abstract:Knowing the actual precipitation in space and time is critical in hydrological modelling applications, yet the spatial coverage with rain gauge stations is limited due to economic constraints. Gridded satellite precipitation datasets offer an alternative option for estimating the actual precipitation by covering uniformly large areas, albeit related estimates are not accurate. To improve precipitation estimates, machine learning is applied to merge rain gauge-based measurements and gridded satellite precipitation products. In this context, observed precipitation plays the role of the dependent variable, while satellite data play the role of predictor variables. Random forests is the dominant machine learning algorithm in relevant applications. In those spatial predictions settings, point predictions (mostly the mean or the median of the conditional distribution) of the dependent variable are issued. Here we propose, issuing probabilistic spatial predictions of precipitation using Light Gradient Boosting Machine (LightGBM). LightGBM is a boosting algorithm, highlighted by prize-winning entries in prediction and forecasting competitions. To assess LightGBM, we contribute a large-scale application that includes merging daily precipitation measurements in contiguous US with PERSIANN and GPM-IMERG satellite precipitation data. We focus on extreme quantiles of the probability distribution of the dependent variable, where LightGBM outperforms quantile regression forests (QRF, a variant of random forests) in terms of quantile score. LightGBM and QRF show similar performance when predicting functionals at the centre of the conditional probability distribution, including the conditional median. Our study offers understanding of probabilistic predictions in spatial settings using machine learning.
Comparison of tree-based ensemble algorithms for merging satellite and earth-observed precipitation data at the daily time scale
Dec 31, 2022Abstract:Merging satellite products and ground-based measurements is often required for obtaining precipitation datasets that simultaneously cover large regions with high density and are more accurate than pure satellite precipitation products. Machine and statistical learning regression algorithms are regularly utilized in this endeavour. At the same time, tree-based ensemble algorithms for regression are adopted in various fields for solving algorithmic problems with high accuracy and low computational cost. The latter can constitute a crucial factor for selecting algorithms for satellite precipitation product correction at the daily and finer time scales, where the size of the datasets is particularly large. Still, information on which tree-based ensemble algorithm to select in such a case for the contiguous United States (US) is missing from the literature. In this work, we conduct an extensive comparison between three tree-based ensemble algorithms, specifically random forests, gradient boosting machines (gbm) and extreme gradient boosting (XGBoost), in the context of interest. We use daily data from the PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) and the IMERG (Integrated Multi-satellitE Retrievals for GPM) gridded datasets. We also use earth-observed precipitation data from the Global Historical Climatology Network daily (GHCNd) database. The experiments refer to the entire contiguous US and additionally include the application of the linear regression algorithm for benchmarking purposes. The results suggest that XGBoost is the best-performing tree-based ensemble algorithm among those compared. They also suggest that IMERG is more useful than PERSIANN in the context investigated.
Comparison of machine learning algorithms for merging gridded satellite and earth-observed precipitation data
Dec 17, 2022Abstract:Gridded satellite precipitation datasets are useful in hydrological applications as they cover large regions with high density. However, they are not accurate in the sense that they do not agree with ground-based measurements. An established means for improving their accuracy is to correct them by adopting machine learning algorithms. The problem is defined as a regression setting, in which the ground-based measurements have the role of the dependent variable and the satellite data are the predictor variables, together with topography factors (e.g., elevation). Most studies of this kind involve a limited number of machine learning algorithms, and are conducted at a small region and for a limited time period. Thus, the results obtained through them are of local importance and do not provide more general guidance and best practices. To provide results that are generalizable and to contribute to the delivery of best practices, we here compare eight state-of-the-art machine learning algorithms in correcting satellite precipitation data for the entire contiguous United States and for a 15-year period. We use monthly data from the PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) gridded dataset, together with monthly earth-observed precipitation data from the Global Historical Climatology Network monthly database, version 2 (GHCNm). The results suggest that extreme gradient boosting (XGBoost) and random forests are the most accurate in terms of the squared error scoring function. The remaining algorithms can be ordered as follows from the best to the worst ones: Bayesian regularized feed-forward neural networks, multivariate adaptive polynomial splines (poly-MARS), gradient boosting machines (gbm), multivariate adaptive regression splines (MARS), feed-forward neural networks and linear regression.
A review of probabilistic forecasting and prediction with machine learning
Sep 17, 2022
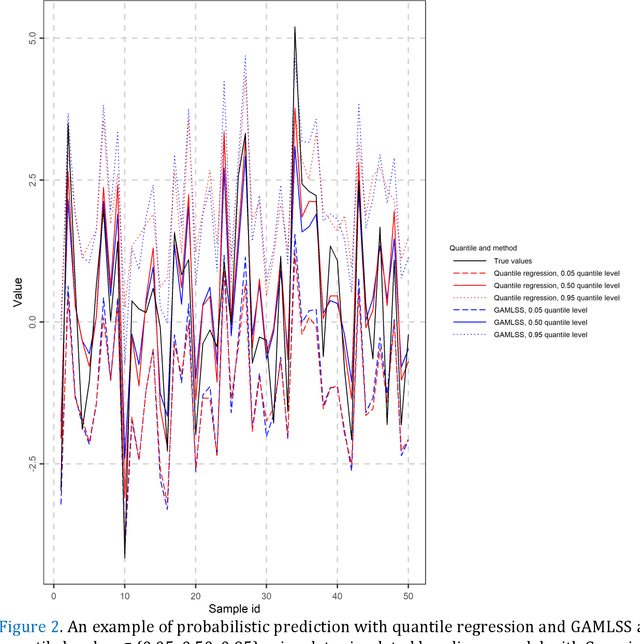
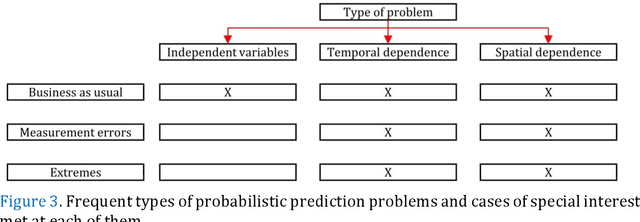
Abstract:Predictions and forecasts of machine learning models should take the form of probability distributions, aiming to increase the quantity of information communicated to end users. Although applications of probabilistic prediction and forecasting with machine learning models in academia and industry are becoming more frequent, related concepts and methods have not been formalized and structured under a holistic view of the entire field. Here, we review the topic of predictive uncertainty estimation with machine learning algorithms, as well as the related metrics (consistent scoring functions and proper scoring rules) for assessing probabilistic predictions. The review covers a time period spanning from the introduction of early statistical (linear regression and time series models, based on Bayesian statistics or quantile regression) to recent machine learning algorithms (including generalized additive models for location, scale and shape, random forests, boosting and deep learning algorithms) that are more flexible by nature. The review of the progress in the field, expedites our understanding on how to develop new algorithms tailored to users' needs, since the latest advancements are based on some fundamental concepts applied to more complex algorithms. We conclude by classifying the material and discussing challenges that are becoming a hot topic of research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge