Efficiency, Fairness, and Stability in Non-Commercial Peer-to-Peer Ridesharing

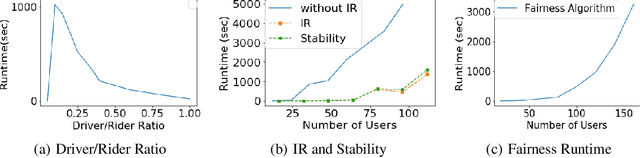
Unlike commercial ridesharing, non-commercial peer-to-peer (P2P) ridesharing has been subject to limited research -- although it can promote viable solutions in non-urban communities. This paper focuses on the core problem in P2P ridesharing: the matching of riders and drivers. We elevate users' preferences as a first-order concern and introduce novel notions of fairness and stability in P2P ridesharing. We propose algorithms for efficient matching while considering user-centric factors, including users' preferred departure time, fairness, and stability. Results suggest that fair and stable solutions can be obtained in reasonable computational times and can improve baseline outcomes based on system-wide efficiency exclusively.

Fairly Allocating Many Goods with Few Queries

We investigate the query complexity of the fair allocation of indivisible goods. For two agents with arbitrary monotonic valuations, we design an algorithm that computes an allocation satisfying envy-freeness up to one good (EF1), a relaxation of envy-freeness, using a logarithmic number of queries. We show that the logarithmic query complexity bound also holds for three agents with additive valuations. These results suggest that it is possible to fairly allocate goods in practice even when the number of goods is extremely large. By contrast, we prove that computing an allocation satisfying envy-freeness and another of its relaxations, envy-freeness up to any good (EFX), requires a linear number of queries even when there are only two agents with identical additive valuations.