Hongfei Liu
Document-level Relation Extraction with Cross-sentence Reasoning Graph
Mar 07, 2023
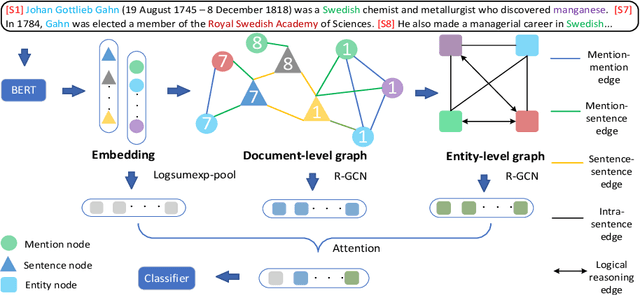
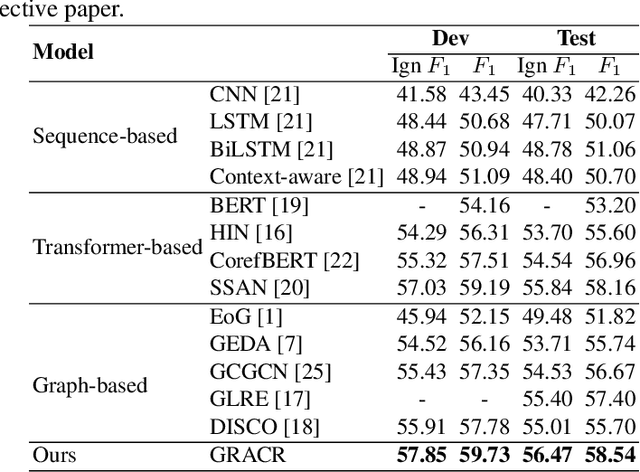

Abstract:Relation extraction (RE) has recently moved from the sentence-level to document-level, which requires aggregating document information and using entities and mentions for reasoning. Existing works put entity nodes and mention nodes with similar representations in a document-level graph, whose complex edges may incur redundant information. Furthermore, existing studies only focus on entity-level reasoning paths without considering global interactions among entities cross-sentence. To these ends, we propose a novel document-level RE model with a GRaph information Aggregation and Cross-sentence Reasoning network (GRACR). Specifically, a simplified document-level graph is constructed to model the semantic information of all mentions and sentences in a document, and an entity-level graph is designed to explore relations of long-distance cross-sentence entity pairs. Experimental results show that GRACR achieves excellent performance on two public datasets of document-level RE. It is especially effective in extracting potential relations of cross-sentence entity pairs. Our code is available at https://github.com/UESTC-LHF/GRACR.
Self-paced Principal Component Analysis
Jun 25, 2021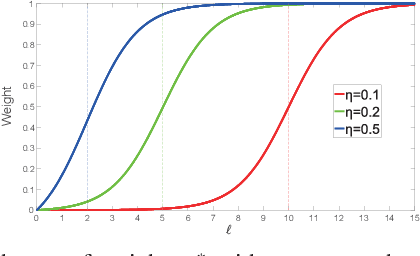



Abstract:Principal Component Analysis (PCA) has been widely used for dimensionality reduction and feature extraction. Robust PCA (RPCA), under different robust distance metrics, such as l1-norm and l2, p-norm, can deal with noise or outliers to some extent. However, real-world data may display structures that can not be fully captured by these simple functions. In addition, existing methods treat complex and simple samples equally. By contrast, a learning pattern typically adopted by human beings is to learn from simple to complex and less to more. Based on this principle, we propose a novel method called Self-paced PCA (SPCA) to further reduce the effect of noise and outliers. Notably, the complexity of each sample is calculated at the beginning of each iteration in order to integrate samples from simple to more complex into training. Based on an alternating optimization, SPCA finds an optimal projection matrix and filters out outliers iteratively. Theoretical analysis is presented to show the rationality of SPCA. Extensive experiments on popular data sets demonstrate that the proposed method can improve the state of-the-art results considerably.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge