Investigation of Frame Differences as Motion Cues for Video Object Segmentation

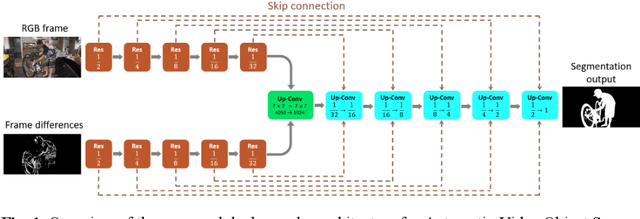
Automatic Video Object Segmentation (AVOS) refers to the task of autonomously segmenting target objects in video sequences without relying on human-provided annotations in the first frames. In AVOS, the use of motion information is crucial, with optical flow being a commonly employed method for capturing motion cues. However, the computation of optical flow is resource-intensive, making it unsuitable for real-time applications, especially on edge devices with limited computational resources. In this study, we propose using frame differences as an alternative to optical flow for motion cue extraction. We developed an extended U-Net-like AVOS model that takes a frame on which segmentation is performed and a frame difference as inputs, and outputs an estimated segmentation map. Our experimental results demonstrate that the proposed model achieves performance comparable to the model with optical flow as an input, particularly when applied to videos captured by stationary cameras. Our results suggest the usefulness of employing frame differences as motion cues in cases with limited computational resources.

From Coupled Oscillators to Graph Neural Networks: Reducing Over-smoothing via a Kuramoto Model-based Approach

We propose the Kuramoto Graph Neural Network (KuramotoGNN), a novel class of continuous-depth graph neural networks (GNNs) that employs the Kuramoto model to mitigate the over-smoothing phenomenon, in which node features in GNNs become indistinguishable as the number of layers increases. The Kuramoto model captures the synchronization behavior of non-linear coupled oscillators. Under the view of coupled oscillators, we first show the connection between Kuramoto model and basic GNN and then over-smoothing phenomenon in GNNs can be interpreted as phase synchronization in Kuramoto model. The KuramotoGNN replaces this phase synchronization with frequency synchronization to prevent the node features from converging into each other while allowing the system to reach a stable synchronized state. We experimentally verify the advantages of the KuramotoGNN over the baseline GNNs and existing methods in reducing over-smoothing on various graph deep learning benchmark tasks.

Sensitivity of quantum PageRank

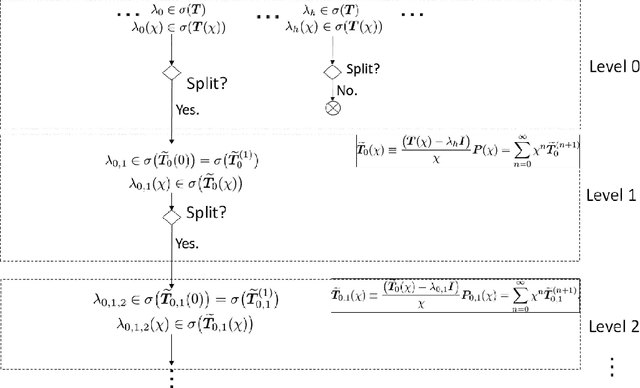
In this paper, we discuss the sensitivity of quantum PageRank. By using the finite dimensional perturbation theory, we estimate the change of the quantum PageRank under a small analytical perturbation on the Google matrix. In addition, we will show the way to estimate the lower bound of the convergence radius as well as the error bound of the finite sum in the expansion of the perturbed PageRank.