Hiromasa Suzuki
Learning Self-Prior for Mesh Inpainting Using Self-Supervised Graph Convolutional Networks
May 01, 2023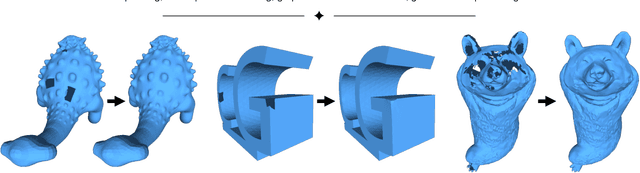
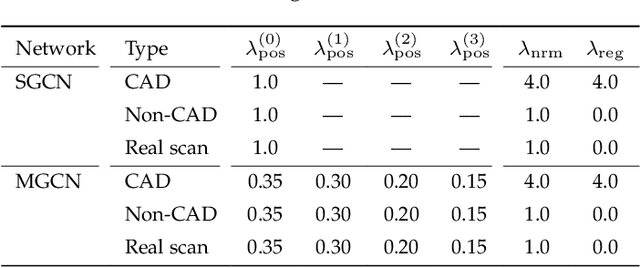
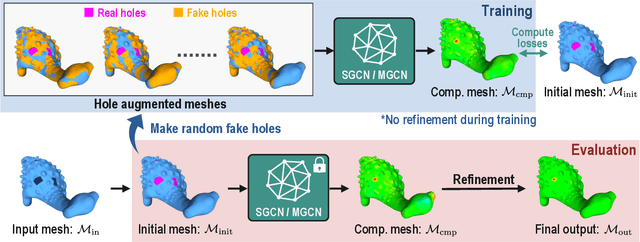
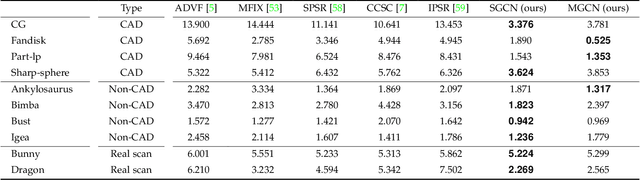
Abstract:This study presents a self-prior-based mesh inpainting framework that requires only an incomplete mesh as input, without the need for any training datasets. Additionally, our method maintains the polygonal mesh format throughout the inpainting process without converting the shape format to an intermediate, such as a voxel grid, a point cloud, or an implicit function, which are typically considered easier for deep neural networks to process. To achieve this goal, we introduce two graph convolutional networks (GCNs): single-resolution GCN (SGCN) and multi-resolution GCN (MGCN), both trained in a self-supervised manner. Our approach refines a watertight mesh obtained from the initial hole filling to generate a completed output mesh. Specifically, we train the GCNs to deform an oversmoothed version of the input mesh into the expected completed shape. To supervise the GCNs for accurate vertex displacements, despite the unknown correct displacements at real holes, we utilize multiple sets of meshes with several connected regions marked as fake holes. The correct displacements are known for vertices in these fake holes, enabling network training with loss functions that assess the accuracy of displacement vectors estimated by the GCNs. We demonstrate that our method outperforms traditional dataset-independent approaches and exhibits greater robustness compared to other deep-learning-based methods for shapes that less frequently appear in shape datasets.
Deep Point-to-Plane Registration by Efficient Backpropagation for Error Minimizing Function
Jul 14, 2022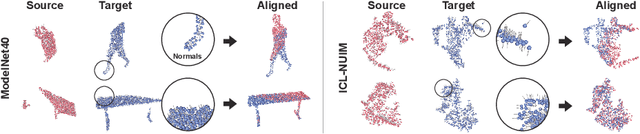
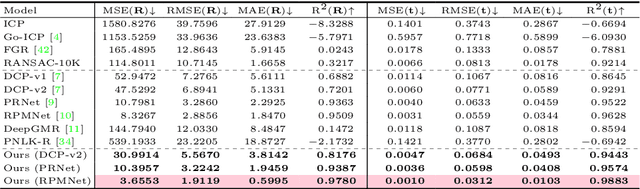

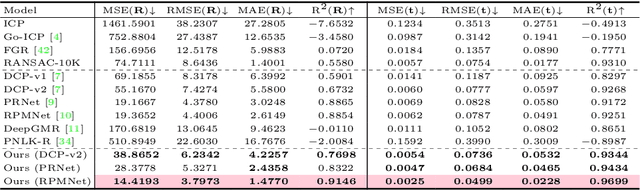
Abstract:Traditional algorithms of point set registration minimizing point-to-plane distances often achieve a better estimation of rigid transformation than those minimizing point-to-point distances. Nevertheless, recent deep-learning-based methods minimize the point-to-point distances. In contrast to these methods, this paper proposes the first deep-learning-based approach to point-to-plane registration. A challenging part of this problem is that a typical solution for point-to-plane registration requires an iterative process of accumulating small transformations obtained by minimizing a linearized energy function. The iteration significantly increases the size of the computation graph needed for backpropagation and can slow down both forward and backward network evaluations. To solve this problem, we consider the estimated rigid transformation as a function of input point clouds and derive its analytic gradients using the implicit function theorem. The analytic gradient that we introduce is independent of how the error minimizing function (i.e., the rigid transformation) is obtained, thus allowing us to calculate both the rigid transformation and its gradient efficiently. We implement the proposed point-to-plane registration module over several previous methods that minimize point-to-point distances and demonstrate that the extensions outperform the base methods even with point clouds with noise and low-quality point normals estimated with local point distributions.
Deep Mesh Prior: Unsupervised Mesh Restoration using Graph Convolutional Networks
Jul 02, 2021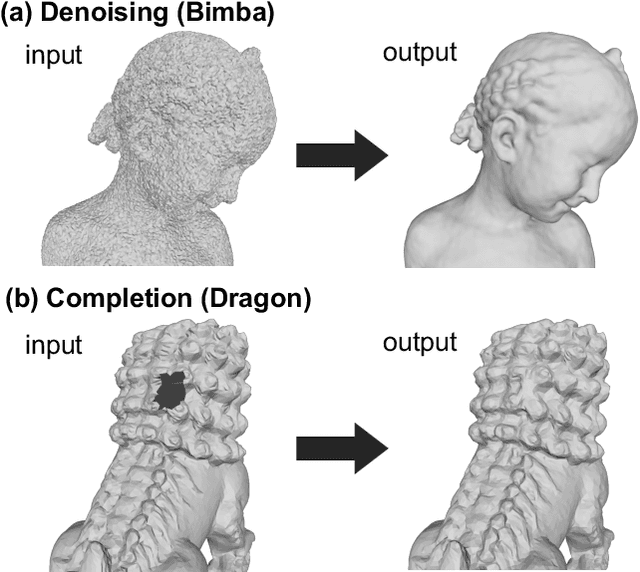
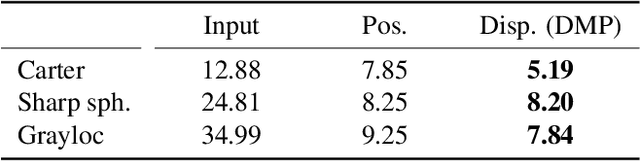
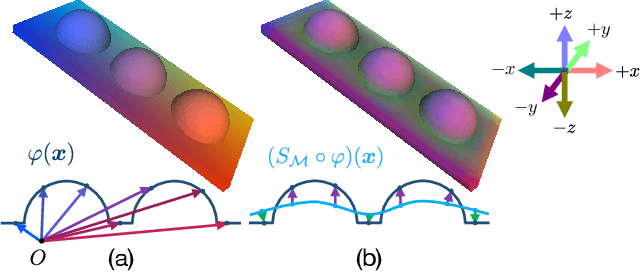

Abstract:This paper addresses mesh restoration problems, i.e., denoising and completion, by learning self-similarity in an unsupervised manner. For this purpose, the proposed method, which we refer to as Deep Mesh Prior, uses a graph convolutional network on meshes to learn the self-similarity. The network takes a single incomplete mesh as input data and directly outputs the reconstructed mesh without being trained using large-scale datasets. Our method does not use any intermediate representations such as an implicit field because the whole process works on a mesh. We demonstrate that our unsupervised method performs equally well or even better than the state-of-the-art methods using large-scale datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge