Hemant Kumar Aggarwal
Display Field-Of-View Agnostic Robust CT Kernel Synthesis Using Model-Based Deep Learning
Feb 19, 2025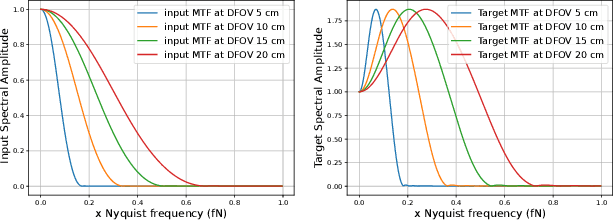

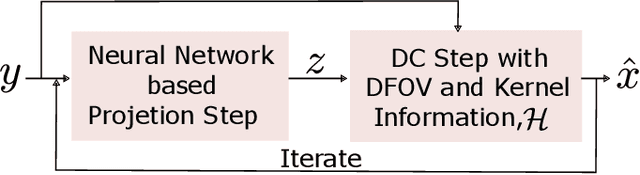
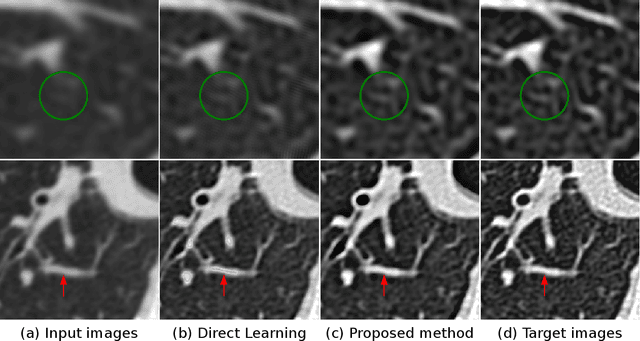
Abstract:In X-ray computed tomography (CT) imaging, the choice of reconstruction kernel is crucial as it significantly impacts the quality of clinical images. Different kernels influence spatial resolution, image noise, and contrast in various ways. Clinical applications involving lung imaging often require images reconstructed with both soft and sharp kernels. The reconstruction of images with different kernels requires raw sinogram data and storing images for all kernels increases processing time and storage requirements. The Display Field-of-View (DFOV) adds complexity to kernel synthesis, as data acquired at different DFOVs exhibit varying levels of sharpness and details. This work introduces an efficient, DFOV-agnostic solution for image-based kernel synthesis using model-based deep learning. The proposed method explicitly integrates CT kernel and DFOV characteristics into the forward model. Experimental results on clinical data, along with quantitative analysis of the estimated modulation transfer function using wire phantom data, clearly demonstrate the utility of the proposed method in real-time. Additionally, a comparative study with a direct learning network, that lacks forward model information, shows that the proposed method is more robust to DFOV variations.
Deep Image Prior using Stein's Unbiased Risk Estimator: SURE-DIP
Nov 21, 2021


Abstract:Deep learning algorithms that rely on extensive training data are revolutionizing image recovery from ill-posed measurements. Training data is scarce in many imaging applications, including ultra-high-resolution imaging. The deep image prior (DIP) algorithm was introduced for single-shot image recovery, completely eliminating the need for training data. A challenge with this scheme is the need for early stopping to minimize the overfitting of the CNN parameters to the noise in the measurements. We introduce a generalized Stein's unbiased risk estimate (GSURE) loss metric to minimize the overfitting. Our experiments show that the SURE-DIP approach minimizes the overfitting issues, thus offering significantly improved performance over classical DIP schemes. We also use the SURE-DIP approach with model-based unrolling architectures, which offers improved performance over direct inversion schemes.
Model Adaptation for Image Reconstruction using Generalized Stein's Unbiased Risk Estimator
Jan 29, 2021



Abstract:Deep learning image reconstruction algorithms often suffer from model mismatches when the acquisition scheme differs significantly from the forward model used during training. We introduce a Generalized Stein's Unbiased Risk Estimate (GSURE) loss metric to adapt the network to the measured k-space data and minimize model misfit impact. Unlike current methods that rely on the mean square error in kspace, the proposed metric accounts for noise in the measurements. This makes the approach less vulnerable to overfitting, thus offering improved reconstruction quality compared to schemes that rely on mean-square error. This approach may be useful to rapidly adapt pre-trained models to new acquisition settings (e.g., multi-site) and different contrasts than training data
ENSURE: Ensemble Stein's Unbiased Risk Estimator for Unsupervised Learning
Oct 20, 2020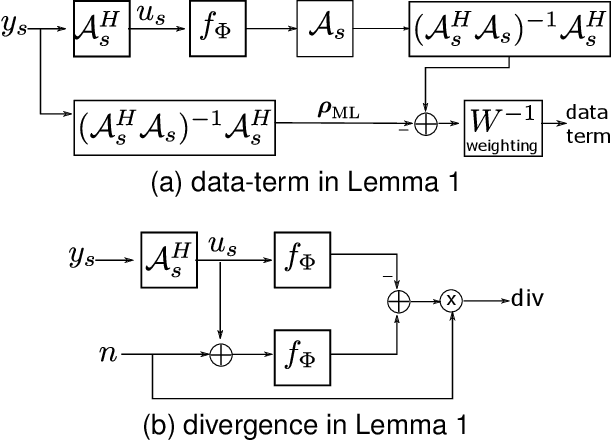
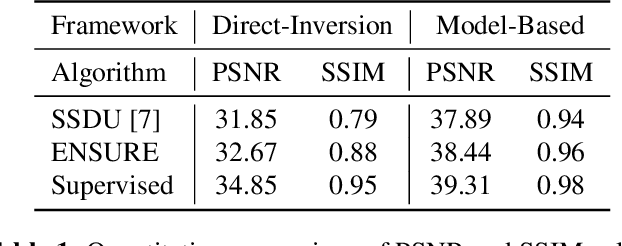
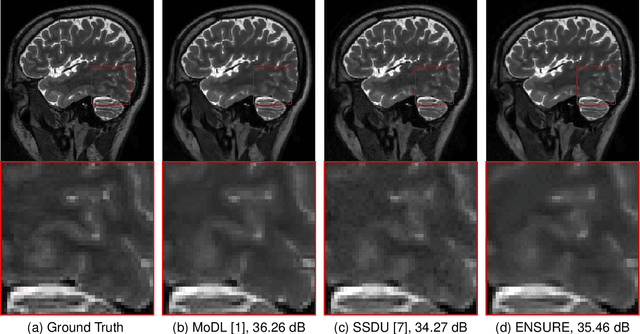
Abstract:Deep learning accelerates the MR image reconstruction process after offline training of a deep neural network from a large volume of clean and fully sampled data. Unfortunately, fully sampled images may not be available or are difficult to acquire in several application areas such as high-resolution imaging. Previous studies have utilized Stein's Unbiased Risk Estimator (SURE) as a mean square error (MSE) estimate for the image denoising problem. Unrolled reconstruction algorithms, where the denoiser at each iteration is trained using SURE, has also been introduced. Unfortunately, the end-to-end training of a network using SURE remains challenging since the projected SURE loss is a poor approximation to the MSE, especially in the heavily undersampled setting. We propose an ENsemble SURE (ENSURE) approach to train a deep network only from undersampled measurements. In particular, we show that training a network using an ensemble of images, each acquired with a different sampling pattern, can closely approximate the MSE. Our preliminary experimental results show that the proposed ENSURE approach gives comparable reconstruction quality to supervised learning and a recent unsupervised learning method.
Joint Optimization of Sampling Patterns and Deep Priors for Improved Parallel MRI
Nov 06, 2019



Abstract:Multichannel imaging techniques are widely used in MRI to reduce the scan time. These schemes typically perform undersampled acquisition and utilize compressed-sensing based regularized reconstruction algorithms. Model-based deep learning (MoDL) frameworks are now emerging as powerful alternatives to compressed sensing, with significantly improved image quality. In this work, we investigate the impact of sampling patterns on the quality of the image recovered using the MoDL algorithm. We introduce a scheme to jointly optimize the sampling pattern and the reconstruction network parameters in MoDL for parallel MRI. The improved decoupling of the network parameters from the sampling patterns offered by the MoDL scheme translates to improved optimization and thus improved performance. Preliminary experimental results demonstrate that the proposed joint optimization framework significantly improves the image quality.
Off-the-grid model based deep learning
Dec 27, 2018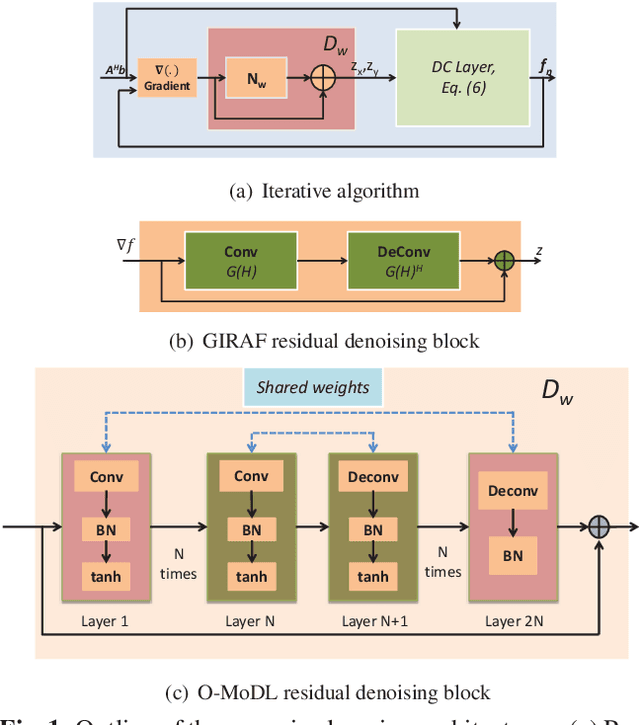
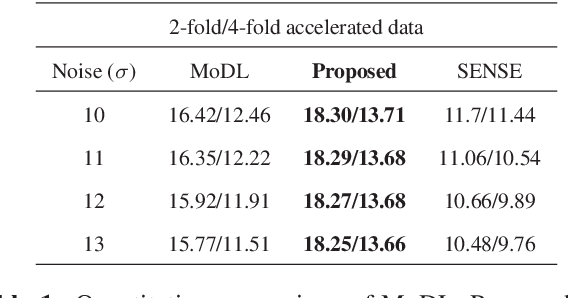
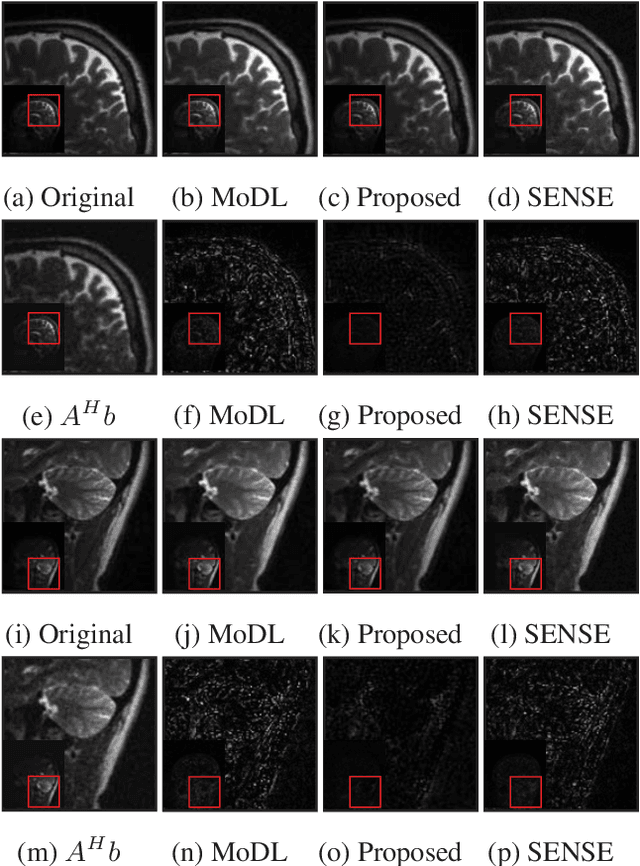
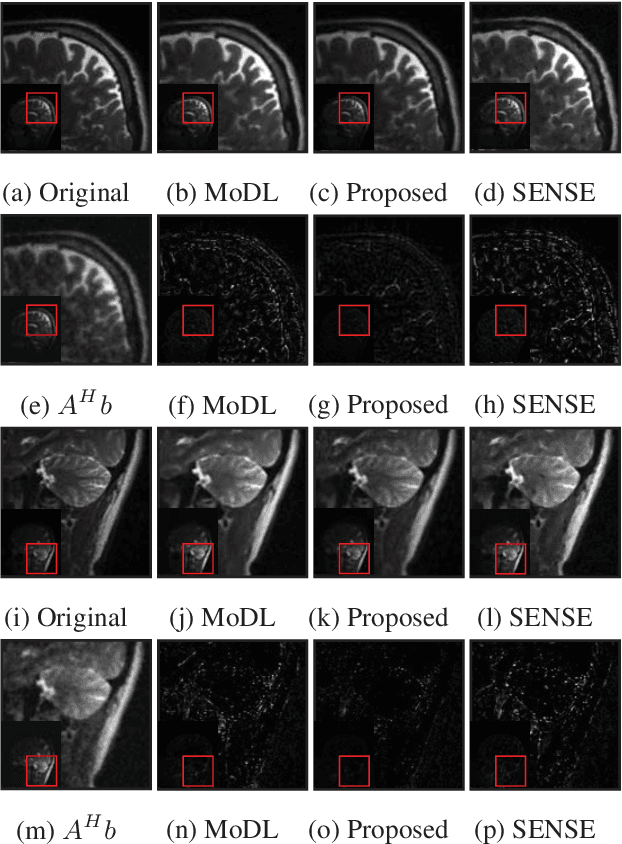
Abstract:We introduce a model based off-the-grid image reconstruction algorithm using deep learned priors. The main difference of the proposed scheme with current deep learning strategies is the learning of non-linear annihilation relations in Fourier space. We rely on a model based framework, which allows us to use a significantly smaller deep network, compared to direct approaches that also learn how to invert the forward model. Preliminary comparisons against image domain MoDL approach demonstrates the potential of the off-the-grid formulation. The main benefit of the proposed scheme compared to structured low-rank methods is the quite significant reduction in computational complexity.
Multi-Shot Sensitivity-Encoded Diffusion MRI using Model-Based Deep Learning (MODL-MUSSELS)
Dec 19, 2018
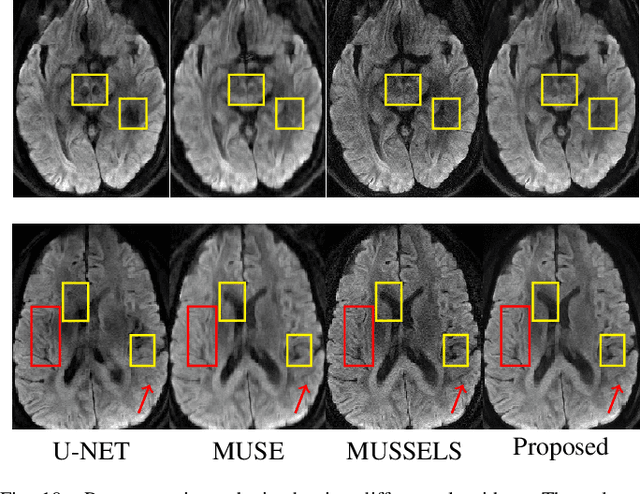
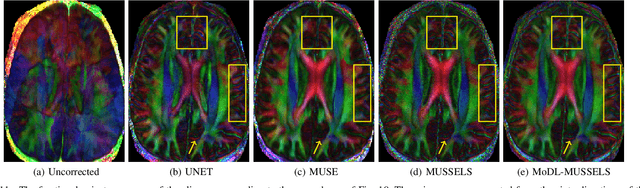
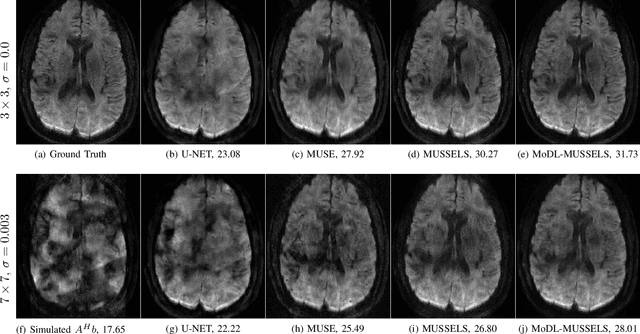
Abstract:We propose a model-based deep learning architecture for the correction of phase errors in multishot diffusion-weighted echo-planar MRI images. This work is a generalization of MUSSELS, which is a structured low-rank algorithm. We show that an iterative reweighted least-squares implementation of MUSSELS resembles the model-based deep learning (MoDL) framework. We propose to replace the self-learned linear filter bank in MUSSELS with a convolutional neural network, whose parameters are learned from exemplary data. The proposed algorithm reduces the computational complexity of MUSSELS by several orders of magnitude while providing comparable image quality.
MoDL: Model Based Deep Learning Architecture for Inverse Problems
Aug 10, 2018


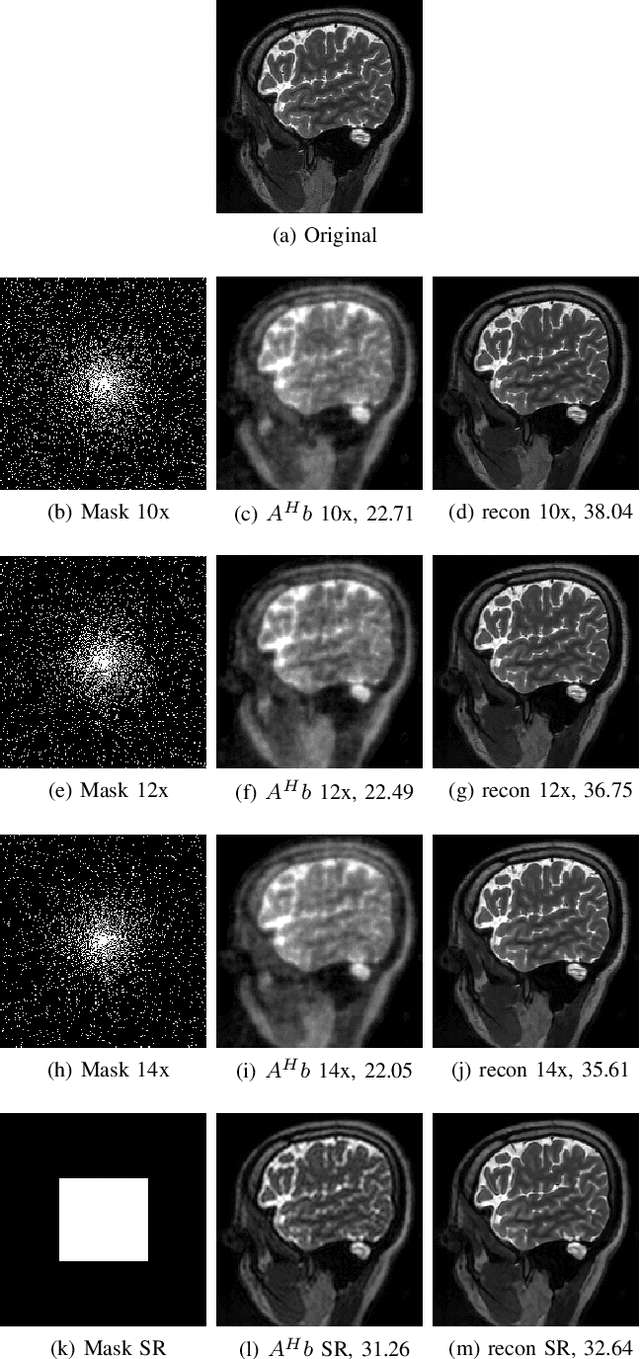
Abstract:We introduce a model-based image reconstruction framework with a convolution neural network (CNN) based regularization prior. The proposed formulation provides a systematic approach for deriving deep architectures for inverse problems with the arbitrary structure. Since the forward model is explicitly accounted for, a smaller network with fewer parameters is sufficient to capture the image information compared to black-box deep learning approaches, thus reducing the demand for training data and training time. Since we rely on end-to-end training, the CNN weights are customized to the forward model, thus offering improved performance over approaches that rely on pre-trained denoisers. The main difference of the framework from existing end-to-end training strategies is the sharing of the network weights across iterations and channels. Our experiments show that the decoupling of the number of iterations from the network complexity offered by this approach provides benefits including lower demand for training data, reduced risk of overfitting, and implementations with significantly reduced memory footprint. We propose to enforce data-consistency by using numerical optimization blocks such as conjugate gradients algorithm within the network; this approach offers faster convergence per iteration, compared to methods that rely on proximal gradients steps to enforce data consistency. Our experiments show that the faster convergence translates to improved performance, especially when the available GPU memory restricts the number of iterations.
Extension of Sparse Randomized Kaczmarz Algorithm for Multiple Measurement Vectors
Feb 02, 2014



Abstract:The Kaczmarz algorithm is popular for iteratively solving an overdetermined system of linear equations. The traditional Kaczmarz algorithm can approximate the solution in few sweeps through the equations but a randomized version of the Kaczmarz algorithm was shown to converge exponentially and independent of number of equations. Recently an algorithm for finding sparse solution to a linear system of equations has been proposed based on weighted randomized Kaczmarz algorithm. These algorithms solves single measurement vector problem; however there are applications were multiple-measurements are available. In this work, the objective is to solve a multiple measurement vector problem with common sparse support by modifying the randomized Kaczmarz algorithm. We have also modeled the problem of face recognition from video as the multiple measurement vector problem and solved using our proposed technique. We have compared the proposed algorithm with state-of-art spectral projected gradient algorithm for multiple measurement vectors on both real and synthetic datasets. The Monte Carlo simulations confirms that our proposed algorithm have better recovery and convergence rate than the MMV version of spectral projected gradient algorithm under fairness constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge