Structured Low-Rank Algorithms: Theory, MR Applications, and Links to Machine Learning

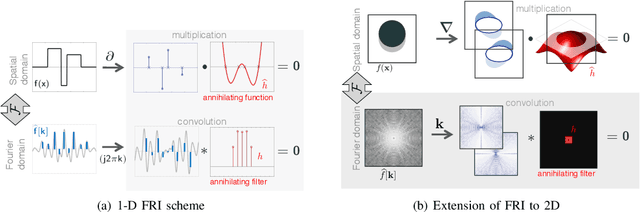
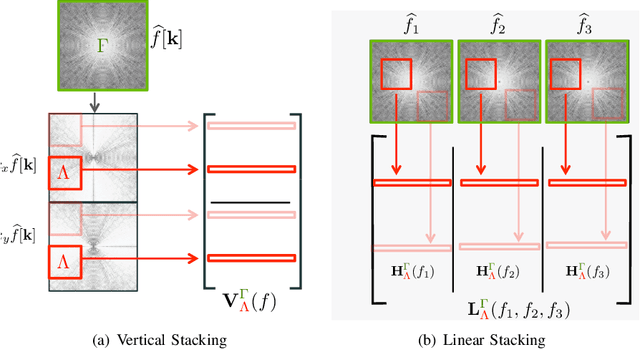
In this survey, we provide a detailed review of recent advances in the recovery of continuous domain multidimensional signals from their few non-uniform (multichannel) measurements using structured low-rank matrix completion formulation. This framework is centered on the fundamental duality between the compactness (e.g., sparsity) of the continuous signal and the rank of a structured matrix, whose entries are functions of the signal. This property enables the reformulation of the signal recovery as a low-rank structured matrix completion, which comes with performance guarantees. We will also review fast algorithms that are comparable in complexity to current compressed sensing methods, which enables the application of the framework to large-scale magnetic resonance (MR) recovery problems. The remarkable flexibility of the formulation can be used to exploit signal properties that are difficult to capture by current sparse and low-rank optimization strategies. We demonstrate the utility of the framework in a wide range of MR imaging (MRI) applications, including highly accelerated imaging, calibration-free acquisition, MR artifact correction, and ungated dynamic MRI.

Multi-Shot Sensitivity-Encoded Diffusion MRI using Model-Based Deep Learning (MODL-MUSSELS)

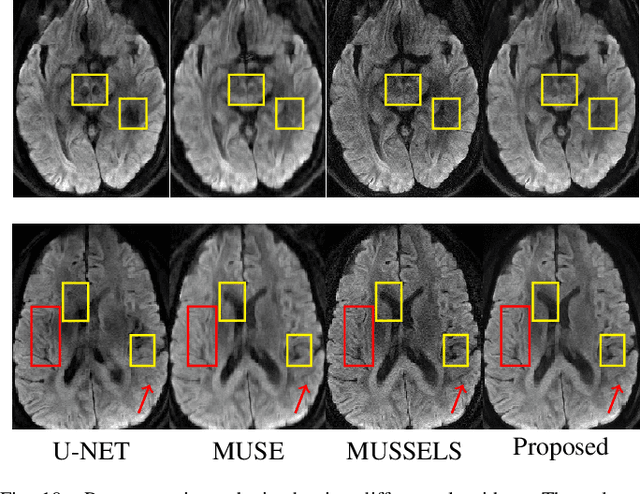
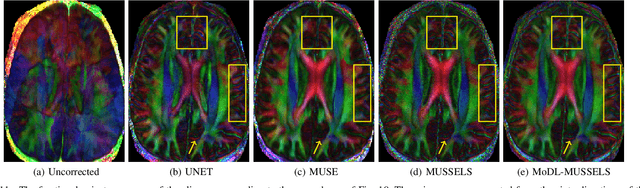
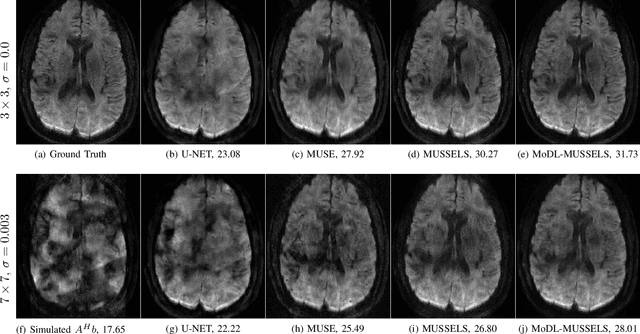
We propose a model-based deep learning architecture for the correction of phase errors in multishot diffusion-weighted echo-planar MRI images. This work is a generalization of MUSSELS, which is a structured low-rank algorithm. We show that an iterative reweighted least-squares implementation of MUSSELS resembles the model-based deep learning (MoDL) framework. We propose to replace the self-learned linear filter bank in MUSSELS with a convolutional neural network, whose parameters are learned from exemplary data. The proposed algorithm reduces the computational complexity of MUSSELS by several orders of magnitude while providing comparable image quality.

MoDL: Model Based Deep Learning Architecture for Inverse Problems

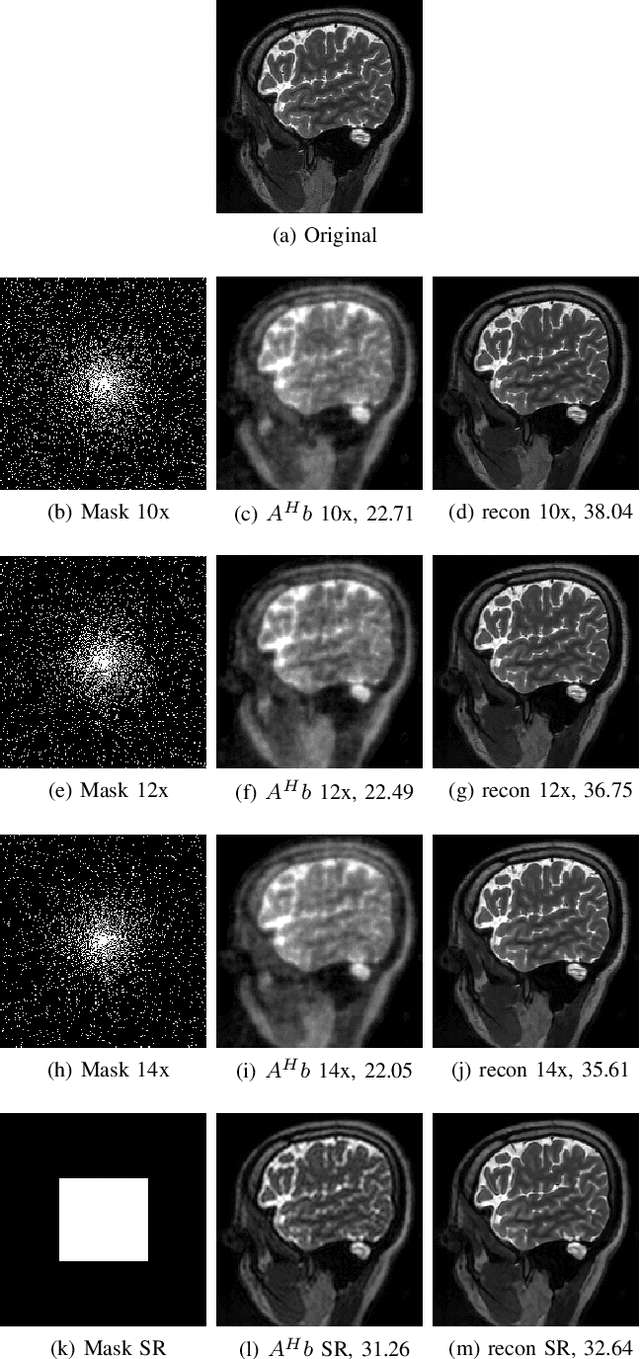
We introduce a model-based image reconstruction framework with a convolution neural network (CNN) based regularization prior. The proposed formulation provides a systematic approach for deriving deep architectures for inverse problems with the arbitrary structure. Since the forward model is explicitly accounted for, a smaller network with fewer parameters is sufficient to capture the image information compared to black-box deep learning approaches, thus reducing the demand for training data and training time. Since we rely on end-to-end training, the CNN weights are customized to the forward model, thus offering improved performance over approaches that rely on pre-trained denoisers. The main difference of the framework from existing end-to-end training strategies is the sharing of the network weights across iterations and channels. Our experiments show that the decoupling of the number of iterations from the network complexity offered by this approach provides benefits including lower demand for training data, reduced risk of overfitting, and implementations with significantly reduced memory footprint. We propose to enforce data-consistency by using numerical optimization blocks such as conjugate gradients algorithm within the network; this approach offers faster convergence per iteration, compared to methods that rely on proximal gradients steps to enforce data consistency. Our experiments show that the faster convergence translates to improved performance, especially when the available GPU memory restricts the number of iterations.