Model-independent variable selection via the rule-based variable priority

While achieving high prediction accuracy is a fundamental goal in machine learning, an equally important task is finding a small number of features with high explanatory power. One popular selection technique is permutation importance, which assesses a variable's impact by measuring the change in prediction error after permuting the variable. However, this can be problematic due to the need to create artificial data, a problem shared by other methods as well. Another problem is that variable selection methods can be limited by being model-specific. We introduce a new model-independent approach, Variable Priority (VarPro), which works by utilizing rules without the need to generate artificial data or evaluate prediction error. The method is relatively easy to use, requiring only the calculation of sample averages of simple statistics, and can be applied to many data settings, including regression, classification, and survival. We investigate the asymptotic properties of VarPro and show, among other things, that VarPro has a consistent filtering property for noise variables. Empirical studies using synthetic and real-world data show the method achieves a balanced performance and compares favorably to many state-of-the-art procedures currently used for variable selection.

A Machine Learning Alternative to P-values

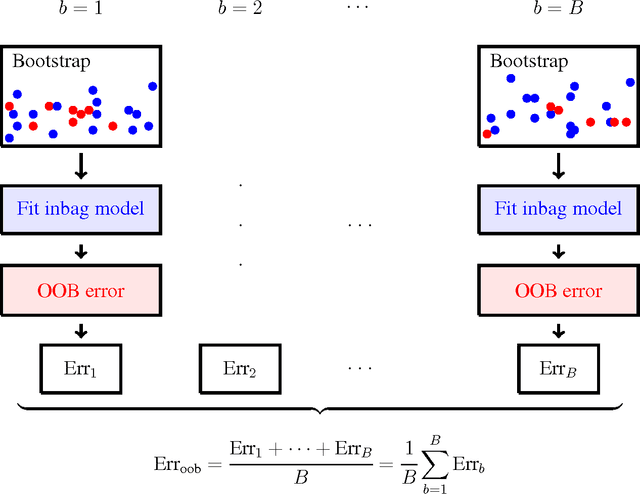
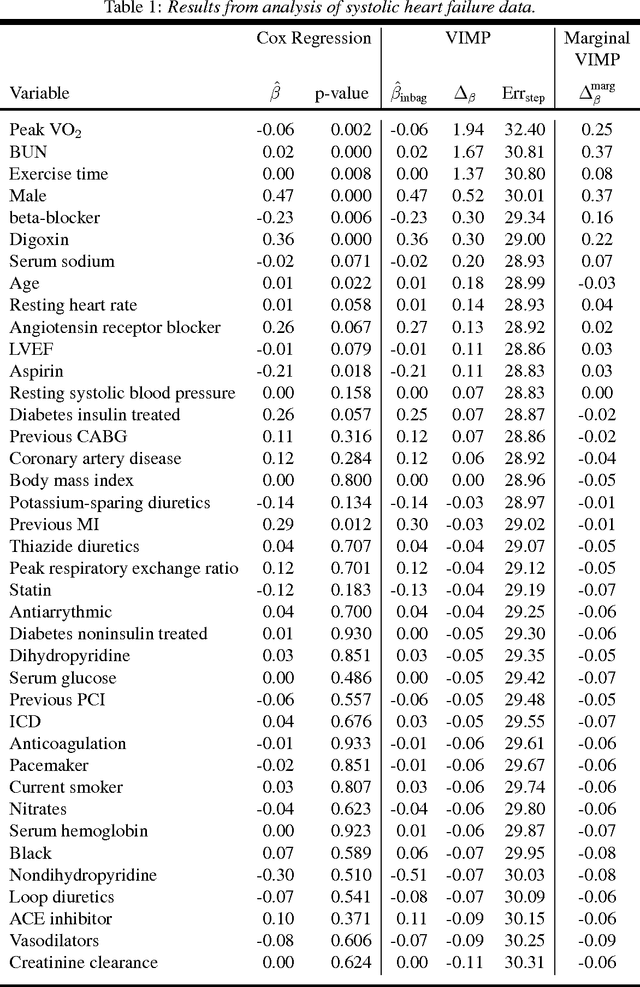
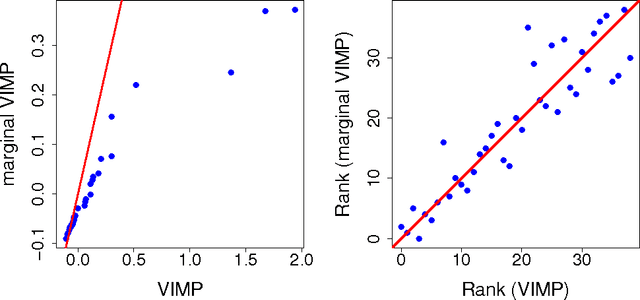
This paper presents an alternative approach to p-values in regression settings. This approach, whose origins can be traced to machine learning, is based on the leave-one-out bootstrap for prediction error. In machine learning this is called the out-of-bag (OOB) error. To obtain the OOB error for a model, one draws a bootstrap sample and fits the model to the in-sample data. The out-of-sample prediction error for the model is obtained by calculating the prediction error for the model using the out-of-sample data. Repeating and averaging yields the OOB error, which represents a robust cross-validated estimate of the accuracy of the underlying model. By a simple modification to the bootstrap data involving "noising up" a variable, the OOB method yields a variable importance (VIMP) index, which directly measures how much a specific variable contributes to the prediction precision of a model. VIMP provides a scientifically interpretable measure of the effect size of a variable, we call the "predictive effect size", that holds whether the researcher's model is correct or not, unlike the p-value whose calculation is based on the assumed correctness of the model. We also discuss a marginal VIMP index, also easily calculated, which measures the marginal effect of a variable, or what we call "the discovery effect". The OOB procedure can be applied to both parametric and nonparametric regression models and requires only that the researcher can repeatedly fit their model to bootstrap and modified bootstrap data. We illustrate this approach on a survival data set involving patients with systolic heart failure and to a simulated survival data set where the model is incorrectly specified to illustrate its robustness to model misspecification.

Estimating Individual Treatment Effect in Observational Data Using Random Forest Methods

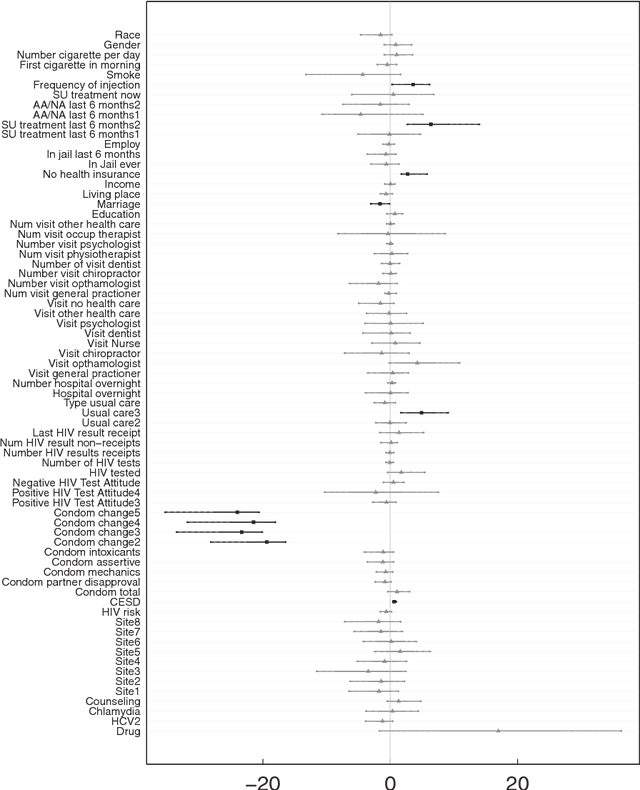
Estimation of individual treatment effect in observational data is complicated due to the challenges of confounding and selection bias. A useful inferential framework to address this is the counterfactual (potential outcomes) model which takes the hypothetical stance of asking what if an individual had received both treatments. Making use of random forests (RF) within the counterfactual framework we estimate individual treatment effects by directly modeling the response. We find accurate estimation of individual treatment effects is possible even in complex heterogeneous settings but that the type of RF approach plays an important role in accuracy. Methods designed to be adaptive to confounding, when used in parallel with out-of-sample estimation, do best. One method found to be especially promising is counterfactual synthetic forests. We illustrate this new methodology by applying it to a large comparative effectiveness trial, Project Aware, in order to explore the role drug use plays in sexual risk. The analysis reveals important connections between risky behavior, drug usage, and sexual risk.

Random Forest Missing Data Algorithms

Random forest (RF) missing data algorithms are an attractive approach for dealing with missing data. They have the desirable properties of being able to handle mixed types of missing data, they are adaptive to interactions and nonlinearity, and they have the potential to scale to big data settings. Currently there are many different RF imputation algorithms but relatively little guidance about their efficacy, which motivated us to study their performance. Using a large, diverse collection of data sets, performance of various RF algorithms was assessed under different missing data mechanisms. Algorithms included proximity imputation, on the fly imputation, and imputation utilizing multivariate unsupervised and supervised splitting---the latter class representing a generalization of a new promising imputation algorithm called missForest. Performance of algorithms was assessed by ability to impute data accurately. Our findings reveal RF imputation to be generally robust with performance improving with increasing correlation. Performance was good under moderate to high missingness, and even (in certain cases) when data was missing not at random.

Variable importance in binary regression trees and forests

We characterize and study variable importance (VIMP) and pairwise variable associations in binary regression trees. A key component involves the node mean squared error for a quantity we refer to as a maximal subtree. The theory naturally extends from single trees to ensembles of trees and applies to methods like random forests. This is useful because while importance values from random forests are used to screen variables, for example they are used to filter high throughput genomic data in Bioinformatics, very little theory exists about their properties.