A Machine Learning Alternative to P-values
Paper and Code
Feb 20, 2017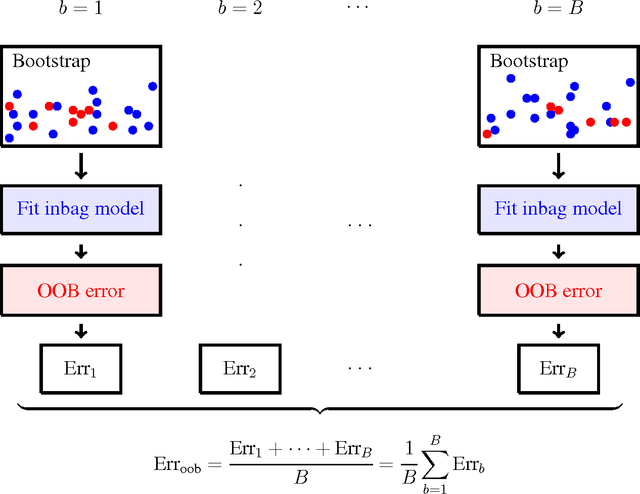
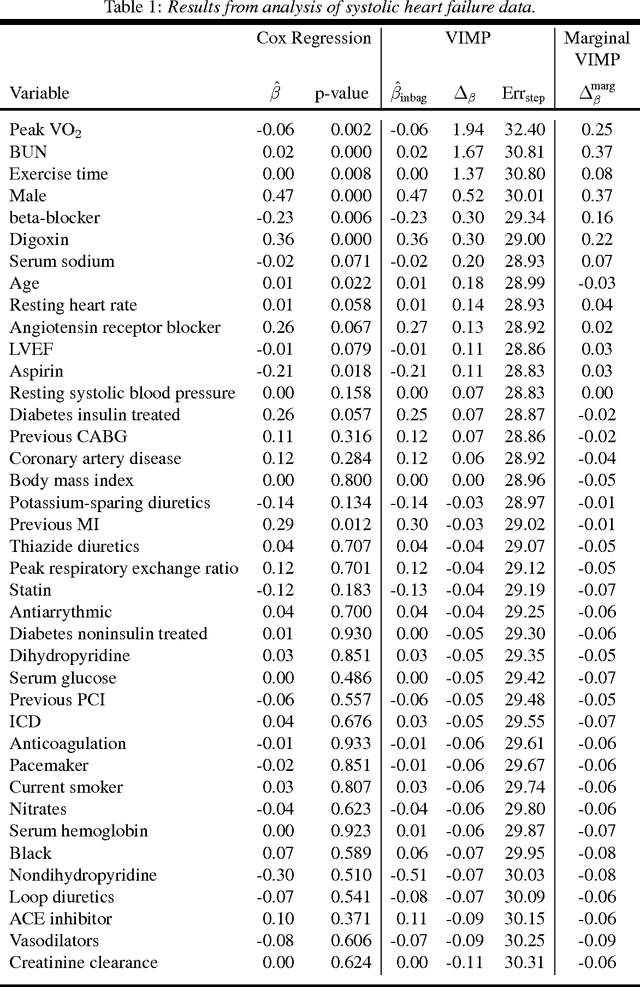

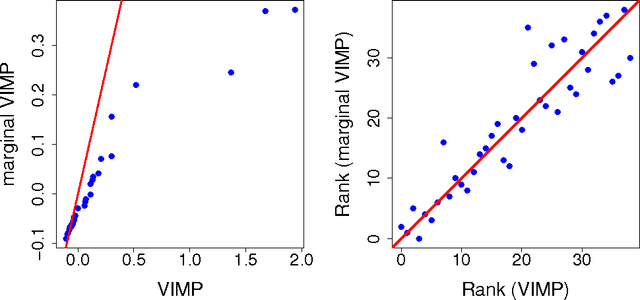
This paper presents an alternative approach to p-values in regression settings. This approach, whose origins can be traced to machine learning, is based on the leave-one-out bootstrap for prediction error. In machine learning this is called the out-of-bag (OOB) error. To obtain the OOB error for a model, one draws a bootstrap sample and fits the model to the in-sample data. The out-of-sample prediction error for the model is obtained by calculating the prediction error for the model using the out-of-sample data. Repeating and averaging yields the OOB error, which represents a robust cross-validated estimate of the accuracy of the underlying model. By a simple modification to the bootstrap data involving "noising up" a variable, the OOB method yields a variable importance (VIMP) index, which directly measures how much a specific variable contributes to the prediction precision of a model. VIMP provides a scientifically interpretable measure of the effect size of a variable, we call the "predictive effect size", that holds whether the researcher's model is correct or not, unlike the p-value whose calculation is based on the assumed correctness of the model. We also discuss a marginal VIMP index, also easily calculated, which measures the marginal effect of a variable, or what we call "the discovery effect". The OOB procedure can be applied to both parametric and nonparametric regression models and requires only that the researcher can repeatedly fit their model to bootstrap and modified bootstrap data. We illustrate this approach on a survival data set involving patients with systolic heart failure and to a simulated survival data set where the model is incorrectly specified to illustrate its robustness to model misspecification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge