Hierarchically Structured Task-Agnostic Continual Learning

One notable weakness of current machine learning algorithms is the poor ability of models to solve new problems without forgetting previously acquired knowledge. The Continual Learning paradigm has emerged as a protocol to systematically investigate settings where the model sequentially observes samples generated by a series of tasks. In this work, we take a task-agnostic view of continual learning and develop a hierarchical information-theoretic optimality principle that facilitates a trade-off between learning and forgetting. We derive this principle from a Bayesian perspective and show its connections to previous approaches to continual learning. Based on this principle, we propose a neural network layer, called the Mixture-of-Variational-Experts layer, that alleviates forgetting by creating a set of information processing paths through the network which is governed by a gating policy. Equipped with a diverse and specialized set of parameters, each path can be regarded as a distinct sub-network that learns to solve tasks. To improve expert allocation, we introduce diversity objectives, which we evaluate in additional ablation studies. Importantly, our approach can operate in a task-agnostic way, i.e., it does not require task-specific knowledge, as is the case with many existing continual learning algorithms. Due to the general formulation based on generic utility functions, we can apply this optimality principle to a large variety of learning problems, including supervised learning, reinforcement learning, and generative modeling. We demonstrate the competitive performance of our method on continual reinforcement learning and variants of the MNIST, CIFAR-10, and CIFAR-100 datasets.

Mixture-of-Variational-Experts for Continual Learning

One significant shortcoming of machine learning is the poor ability of models to solve new problems quicker and without forgetting acquired knowledge. To better understand this issue, continual learning has emerged to systematically investigate learning protocols where the model sequentially observes samples generated by a series of tasks. First, we propose an optimality principle that facilitates a trade-off between learning and forgetting. We derive this principle from an information-theoretic formulation of bounded rationality and show its connections to other continual learning methods. Second, based on this principle, we propose a neural network layer for continual learning, called Mixture-of-Variational-Experts (MoVE), that alleviates forgetting while enabling the beneficial transfer of knowledge to new tasks. Our experiments on variants of the MNIST and CIFAR10 datasets demonstrate the competitive performance of MoVE layers when compared to state-of-the-art approaches.

Binary Classification: Counterbalancing Class Imbalance by Applying Regression Models in Combination with One-Sided Label Shifts

In many real-world pattern recognition scenarios, such as in medical applications, the corresponding classification tasks can be of an imbalanced nature. In the current study, we focus on binary, imbalanced classification tasks, i.e.~binary classification tasks in which one of the two classes is under-represented (minority class) in comparison to the other class (majority class). In the literature, many different approaches have been proposed, such as under- or oversampling, to counter class imbalance. In the current work, we introduce a novel method, which addresses the issues of class imbalance. To this end, we first transfer the binary classification task to an equivalent regression task. Subsequently, we generate a set of negative and positive target labels, such that the corresponding regression task becomes balanced, with respect to the redefined target label set. We evaluate our approach on a number of publicly available data sets in combination with Support Vector Machines. Moreover, we compare our proposed method to one of the most popular oversampling techniques (SMOTE). Based on the detailed discussion of the presented outcomes of our experimental evaluation, we provide promising ideas for future research directions.

Specialization in Hierarchical Learning Systems

Joining multiple decision-makers together is a powerful way to obtain more sophisticated decision-making systems, but requires to address the questions of division of labor and specialization. We investigate in how far information constraints in hierarchies of experts not only provide a principled method for regularization but also to enforce specialization. In particular, we devise an information-theoretically motivated on-line learning rule that allows partitioning of the problem space into multiple sub-problems that can be solved by the individual experts. We demonstrate two different ways to apply our method: (i) partitioning problems based on individual data samples and (ii) based on sets of data samples representing tasks. Approach (i) equips the system with the ability to solve complex decision-making problems by finding an optimal combination of local expert decision-makers. Approach (ii) leads to decision-makers specialized in solving families of tasks, which equips the system with the ability to solve meta-learning problems. We show the broad applicability of our approach on a range of problems including classification, regression, density estimation, and reinforcement learning problems, both in the standard machine learning setup and in a meta-learning setting.

Hierarchical Expert Networks for Meta-Learning

The goal of meta-learning is to train a model on a variety of learning tasks, such that it can adapt to new problems within only a few iterations. Here we propose a principled information-theoretic model that optimally partitions the underlying problem space such that the resulting partitions are processed by specialized expert decision-makers. To drive this specialization we impose the same kind of information processing constraints both on the partitioning and the expert decision-makers. We argue that this specialization leads to efficient adaptation to new tasks. To demonstrate the generality of our approach we evaluate on three meta-learning domains: image classification, regression, and reinforcement learning.

An Information-theoretic On-line Learning Principle for Specialization in Hierarchical Decision-Making Systems

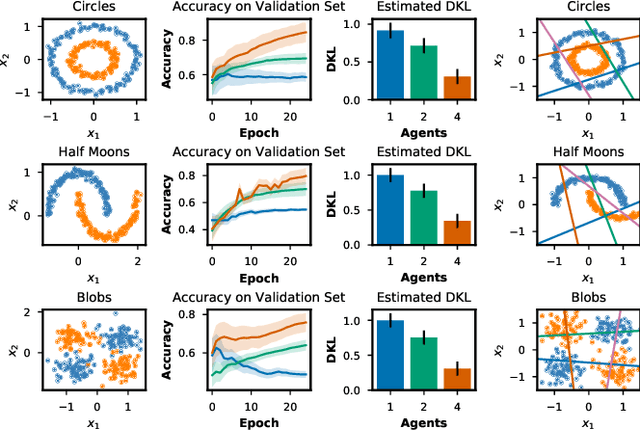
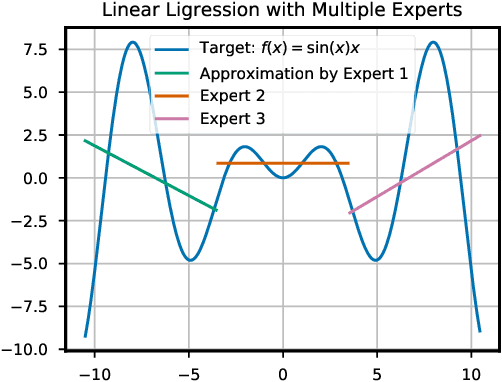
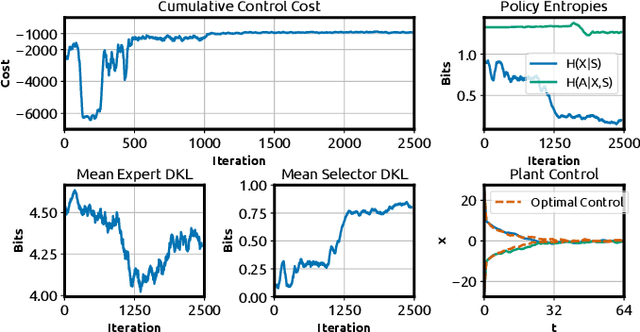
Information-theoretic bounded rationality describes utility-optimizing decision-makers whose limited information-processing capabilities are formalized by information constraints. One of the consequences of bounded rationality is that resource-limited decision-makers can join together to solve decision-making problems that are beyond the capabilities of each individual. Here, we study an information-theoretic principle that drives division of labor and specialization when decision-makers with information constraints are joined together. We devise an on-line learning rule of this principle that learns a partitioning of the problem space such that it can be solved by specialized linear policies. We demonstrate the approach for decision-making problems whose complexity exceeds the capabilities of individual decision-makers, but can be solved by combining the decision-makers optimally. The strength of the model is that it is abstract and principled, yet has direct applications in classification, regression, reinforcement learning and adaptive control.

Bounded Rational Decision-Making with Adaptive Neural Network Priors

Bounded rationality investigates utility-optimizing decision-makers with limited information-processing power. In particular, information theoretic bounded rationality models formalize resource constraints abstractly in terms of relative Shannon information, namely the Kullback-Leibler Divergence between the agents' prior and posterior policy. Between prior and posterior lies an anytime deliberation process that can be instantiated by sample-based evaluations of the utility function through Markov Chain Monte Carlo (MCMC) optimization. The most simple model assumes a fixed prior and can relate abstract information-theoretic processing costs to the number of sample evaluations. However, more advanced models would also address the question of learning, that is how the prior is adapted over time such that generated prior proposals become more efficient. In this work we investigate generative neural networks as priors that are optimized concurrently with anytime sample-based decision-making processes such as MCMC. We evaluate this approach on toy examples.