An Information-theoretic On-line Learning Principle for Specialization in Hierarchical Decision-Making Systems
Paper and Code
Jul 26, 2019
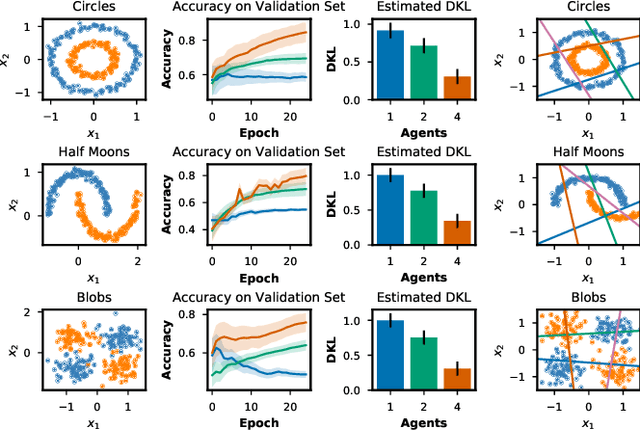
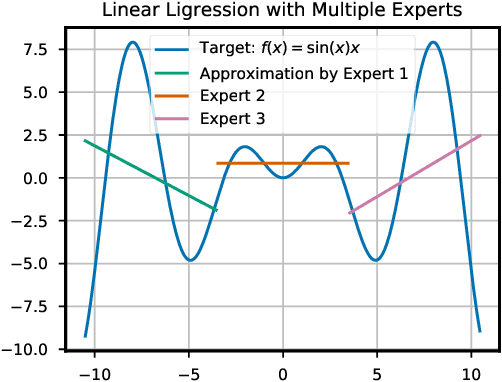
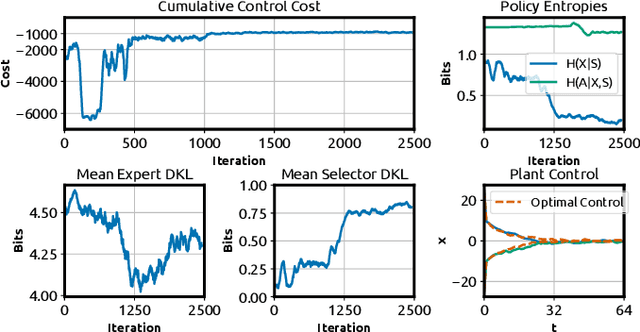
Information-theoretic bounded rationality describes utility-optimizing decision-makers whose limited information-processing capabilities are formalized by information constraints. One of the consequences of bounded rationality is that resource-limited decision-makers can join together to solve decision-making problems that are beyond the capabilities of each individual. Here, we study an information-theoretic principle that drives division of labor and specialization when decision-makers with information constraints are joined together. We devise an on-line learning rule of this principle that learns a partitioning of the problem space such that it can be solved by specialized linear policies. We demonstrate the approach for decision-making problems whose complexity exceeds the capabilities of individual decision-makers, but can be solved by combining the decision-makers optimally. The strength of the model is that it is abstract and principled, yet has direct applications in classification, regression, reinforcement learning and adaptive control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge