The Secretary Problem with Predictions and a Chosen Order

We study a learning-augmented variant of the secretary problem, recently introduced by Fujii and Yoshida (2023), in which the decision-maker has access to machine-learned predictions of candidate values. The central challenge is to balance consistency and robustness: when predictions are accurate, the algorithm should select a near-optimal secretary, while under inaccurate predictions it should still guarantee a bounded competitive ratio. We consider both the classical Random Order Secretary Problem (ROSP), where candidates arrive in a uniformly random order, and a more natural learning-augmented model in which the decision-maker may choose the arrival order based on predicted values. We call this model the Chosen Order Secretary Problem (COSP), capturing scenarios such as interview schedules set in advance. We propose a new randomized algorithm applicable to both ROSP and COSP. Our method switches from fully trusting predictions to a threshold-based rule once a large prediction deviation is detected. Let $ε\in [0,1]$ denote the maximum multiplicative prediction error. For ROSP, our algorithm achieves a competitive ratio of $\max\{0.221, (1-ε)/(1+ε)\}$, improving upon the prior bound of $\max\{0.215, (1-ε)/(1+ε)\}$. For COSP, we achieve $\max\{0.262, (1-ε)/(1+ε)\}$, surpassing the $0.25$ worst-case bound for prior approaches and moving closer to the classical secretary benchmark of $1/e \approx 0.368$. These results highlight the benefit of combining predictions with arrival-order control in online decision-making.

Learning Revenue Maximizing Menus of Lotteries and Two-Part Tariffs

We study learnability of two important classes of mechanisms, menus of lotteries and two-part tariffs. A menu of lotteries is a list of entries where each entry is a pair consisting of probabilities of allocating each item and a price. Menus of lotteries is an especially important family of randomized mechanisms that are known to achieve revenue beyond any deterministic mechanism. A menu of two-part tariffs, on the other hand, is a pricing scheme (that consists of an up-front fee and a per unit fee) that is commonly used in the real world, e.g., for car or bike sharing services. We study learning high-revenue menus of lotteries and two-part tariffs from buyer valuation data in both distributional settings, where we have access to buyers' valuation samples up-front, and online settings, where buyers arrive one at a time and no distributional assumption is made about their values. Our main contribution is proposing the first online learning algorithms for menus of lotteries and two-part tariffs with strong regret bound guarantees. Furthermore, we provide algorithms with improved running times over prior work for the distributional settings. The key difficulty when deriving learning algorithms for these settings is that the relevant revenue functions have sharp transition boundaries. In stark contrast with the recent literature on learning such unstructured functions, we show that simple discretization-based techniques are sufficient for learning in these settings.

Setting Fair Incentives to Maximize Improvement

We consider the problem of helping agents improve by setting short-term goals. Given a set of target skill levels, we assume each agent will try to improve from their initial skill level to the closest target level within reach or do nothing if no target level is within reach. We consider two models: the common improvement capacity model, where agents have the same limit on how much they can improve, and the individualized improvement capacity model, where agents have individualized limits. Our goal is to optimize the target levels for social welfare and fairness objectives, where social welfare is defined as the total amount of improvement, and fairness objectives are considered where the agents belong to different underlying populations. A key technical challenge of this problem is the non-monotonicity of social welfare in the set of target levels, i.e., adding a new target level may decrease the total amount of improvement as it may get easier for some agents to improve. This is especially challenging when considering multiple groups because optimizing target levels in isolation for each group and outputting the union may result in arbitrarily low improvement for a group, failing the fairness objective. Considering these properties, we provide algorithms for optimal and near-optimal improvement for both social welfare and fairness objectives. These algorithmic results work for both the common and individualized improvement capacity models. Furthermore, we show a placement of target levels exists that is approximately optimal for the social welfare of each group. Unlike the algorithmic results, this structural statement only holds in the common improvement capacity model, and we show counterexamples in the individualized improvement capacity model. Finally, we extend our algorithms to learning settings where we have only sample access to the initial skill levels of agents.

On classification of strategic agents who can both game and improve

In this work, we consider classification of agents who can both game and improve. For example, people wishing to get a loan may be able to take some actions that increase their perceived credit-worthiness and others that also increase their true credit-worthiness. A decision-maker would like to define a classification rule with few false-positives (does not give out many bad loans) while yielding many true positives (giving out many good loans), which includes encouraging agents to improve to become true positives if possible. We consider two models for this problem, a general discrete model and a linear model, and prove algorithmic, learning, and hardness results for each. For the general discrete model, we give an efficient algorithm for the problem of maximizing the number of true positives subject to no false positives, and show how to extend this to a partial-information learning setting. We also show hardness for the problem of maximizing the number of true positives subject to a nonzero bound on the number of false positives, and that this hardness holds even for a finite-point version of our linear model. We also show that maximizing the number of true positives subject to no false positive is NP-hard in our full linear model. We additionally provide an algorithm that determines whether there exists a linear classifier that classifies all agents accurately and causes all improvable agents to become qualified, and give additional results for low-dimensional data.

The Strategic Perceptron

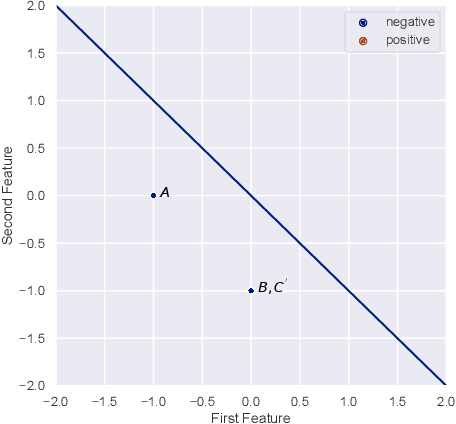
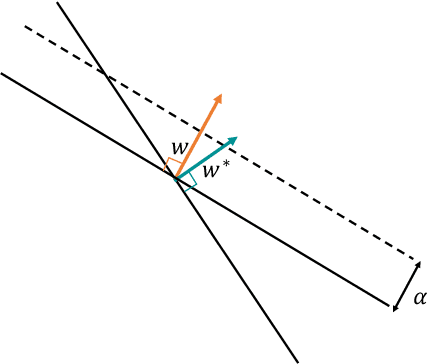
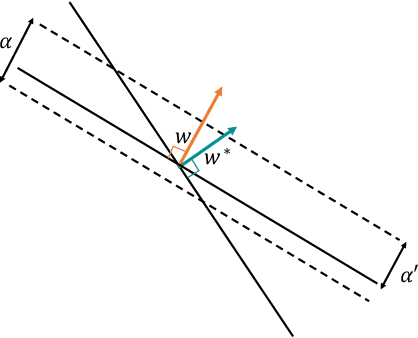
The classical Perceptron algorithm provides a simple and elegant procedure for learning a linear classifier. In each step, the algorithm observes the sample's position and label and may update the current predictor accordingly. In presence of strategic agents, however, the classifier may not be able to observe the true position but a position where the agent pretends to be in order to be classified desirably. Unlike the original setting with perfect knowledge of positions, in this situation the Perceptron algorithm fails to achieve its guarantees, and we illustrate examples with the predictor oscillating between two solutions forever, never reaching a perfect classifier even though one exists. Our main contribution is providing a modified Perceptron-style algorithm which finds a classifier in presence of strategic agents with both $\ell_2$ and weighted $\ell_1$ manipulation costs. In our baseline model, knowledge of the manipulation costs is assumed. In our most general model, we relax this assumption and provide an algorithm which learns and refines both the classifier and its cost estimates to achieve good mistake bounds even when manipulation costs are unknown.