The Strategic Perceptron

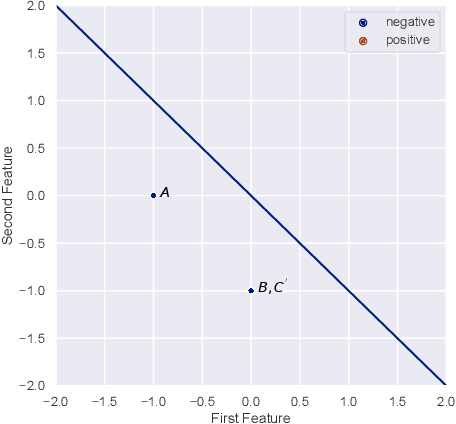
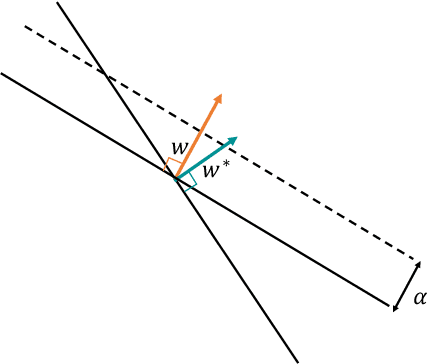
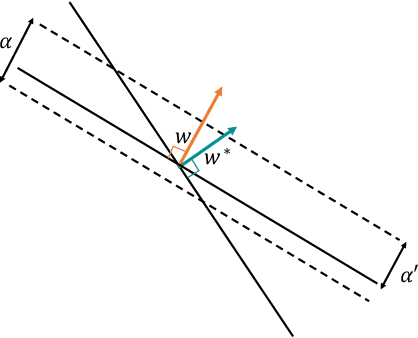
The classical Perceptron algorithm provides a simple and elegant procedure for learning a linear classifier. In each step, the algorithm observes the sample's position and label and may update the current predictor accordingly. In presence of strategic agents, however, the classifier may not be able to observe the true position but a position where the agent pretends to be in order to be classified desirably. Unlike the original setting with perfect knowledge of positions, in this situation the Perceptron algorithm fails to achieve its guarantees, and we illustrate examples with the predictor oscillating between two solutions forever, never reaching a perfect classifier even though one exists. Our main contribution is providing a modified Perceptron-style algorithm which finds a classifier in presence of strategic agents with both $\ell_2$ and weighted $\ell_1$ manipulation costs. In our baseline model, knowledge of the manipulation costs is assumed. In our most general model, we relax this assumption and provide an algorithm which learns and refines both the classifier and its cost estimates to achieve good mistake bounds even when manipulation costs are unknown.