Hedda Cohen Indelman
CSG: A Context-Semantic Guided Diffusion Approach in De Novo Musculoskeletal Ultrasound Image Generation
Dec 08, 2024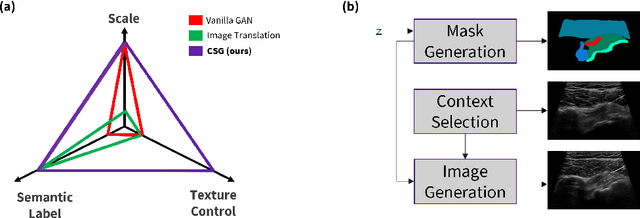
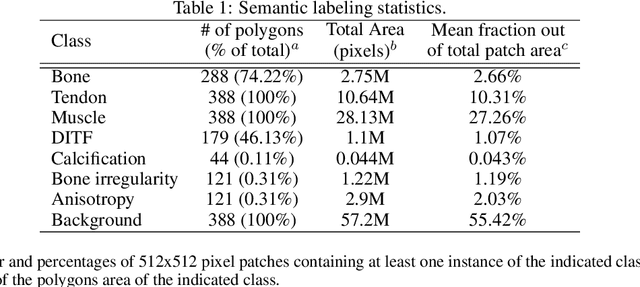
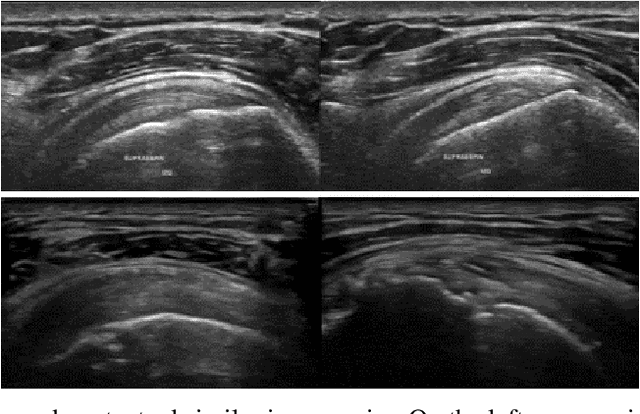
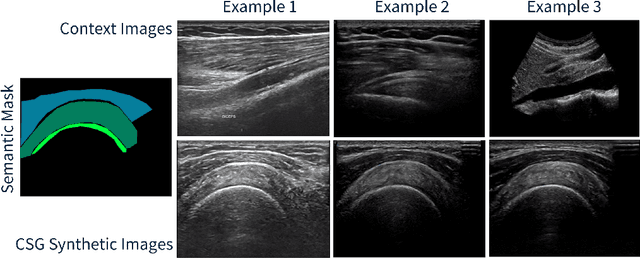
Abstract:The use of synthetic images in medical imaging Artificial Intelligence (AI) solutions has been shown to be beneficial in addressing the limited availability of diverse, unbiased, and representative data. Despite the extensive use of synthetic image generation methods, controlling the semantics variability and context details remains challenging, limiting their effectiveness in producing diverse and representative medical image datasets. In this work, we introduce a scalable semantic and context-conditioned generative model, coined CSG (Context-Semantic Guidance). This dual conditioning approach allows for comprehensive control over both structure and appearance, advancing the synthesis of realistic and diverse ultrasound images. We demonstrate the ability of CSG to generate findings (pathological anomalies) in musculoskeletal (MSK) ultrasound images. Moreover, we test the quality of the synthetic images using a three-fold validation protocol. The results show that the synthetic images generated by CSG improve the performance of semantic segmentation models, exhibit enhanced similarity to real images compared to the baseline methods, and are undistinguishable from real images according to a Turing test. Furthermore, we demonstrate an extension of the CSG that allows enhancing the variability space of images by synthetically generating augmentations of anatomical geometries and textures.
On The Statistical Representation Properties Of The Perturb-Softmax And The Perturb-Argmax Probability Distributions
Jun 04, 2024Abstract:The Gumbel-Softmax probability distribution allows learning discrete tokens in generative learning, while the Gumbel-Argmax probability distribution is useful in learning discrete structures in discriminative learning. Despite the efforts invested in optimizing these probability models, their statistical properties are under-explored. In this work, we investigate their representation properties and determine for which families of parameters these probability distributions are complete, i.e., can represent any probability distribution, and minimal, i.e., can represent a probability distribution uniquely. We rely on convexity and differentiability to determine these statistical conditions and extend this framework to general probability models, such as Gaussian-Softmax and Gaussian-Argmax. We experimentally validate the qualities of these extensions, which enjoy a faster convergence rate. We conclude the analysis by identifying two sets of parameters that satisfy these assumptions and thus admit a complete and minimal representation. Our contribution is theoretical with supporting practical evaluation.
Semantic Segmentation Refiner for Ultrasound Applications with Zero-Shot Foundation Models
Apr 25, 2024Abstract:Despite the remarkable success of deep learning in medical imaging analysis, medical image segmentation remains challenging due to the scarcity of high-quality labeled images for supervision. Further, the significant domain gap between natural and medical images in general and ultrasound images in particular hinders fine-tuning models trained on natural images to the task at hand. In this work, we address the performance degradation of segmentation models in low-data regimes and propose a prompt-less segmentation method harnessing the ability of segmentation foundation models to segment abstract shapes. We do that via our novel prompt point generation algorithm which uses coarse semantic segmentation masks as input and a zero-shot prompt-able foundation model as an optimization target. We demonstrate our method on a segmentation findings task (pathologic anomalies) in ultrasound images. Our method's advantages are brought to light in varying degrees of low-data regime experiments on a small-scale musculoskeletal ultrasound images dataset, yielding a larger performance gain as the training set size decreases.
Learning Randomly Perturbed Structured Predictors for Direct Loss Minimization
Jul 11, 2020



Abstract:Direct loss minimization is a popular approach for learning predictors over structured label spaces. This approach is computationally appealing as it replaces integration with optimization and allows to propagate gradients in a deep net using loss-perturbed prediction. Recently, this technique was extended to generative models, while introducing a randomized predictor that samples a structure from a randomly perturbed score function. In this work, we learn the variance of these randomized structured predictors and show that it balances better between the learned score function and the randomized noise in structured prediction. We demonstrate empirically the effectiveness of learning the balance between the signal and the random noise in structured discrete spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge