MorphoCopter: Design, Modeling, and Control of a New Transformable Quad-Bi Copter

This paper presents a novel morphing quadrotor, named MorphoCopter, covering its design, modeling, control, and experimental tests. It features a unique single rotary joint that enables rapid transformation into an ultra-narrow profile. Although quadrotors have seen widespread adoption in applications such as cinematography, agriculture, and disaster management with increasingly sophisticated control systems, their hardware configurations have remained largely unchanged, limiting their capabilities in certain environments. Our design addresses this by enabling the hardware configuration to change on the fly when required. In standard flight mode, the MorphoCopter adopts an X configuration, functioning as a traditional quadcopter, but can quickly fold into a stacked bicopters arrangement or any configuration in between. Existing morphing designs often sacrifice controllability in compact configurations or rely on complex multi-joint systems. Moreover, our design achieves a greater width reduction than any existing solution. We develop a new inertia and control-action aware adaptive control system that maintains robust performance across all rotary-joint configurations. The prototype can reduce its width from 447 mm to 138 mm (nearly 70\% reduction) in just a few seconds. We validated the MorphoCopter through rigorous simulations and a comprehensive series of flight experiments, including robustness tests, trajectory tracking, and narrow-gap passing tests.

Improving Disturbance Estimation and Suppression via Learning among Systems with Mismatched Dynamics

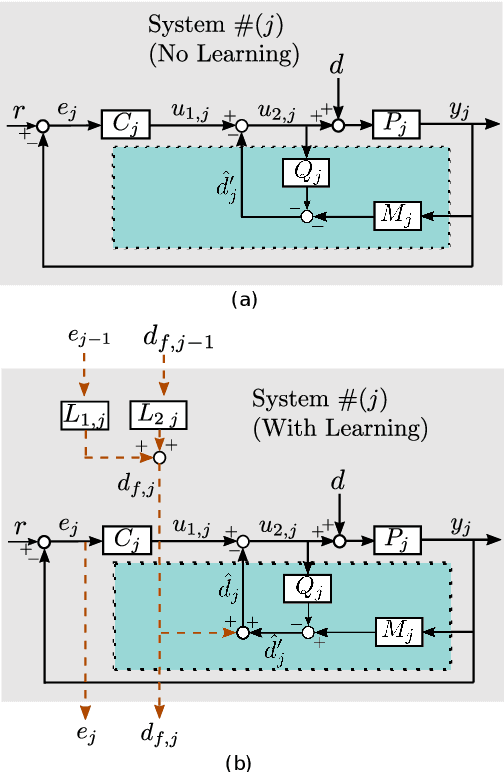
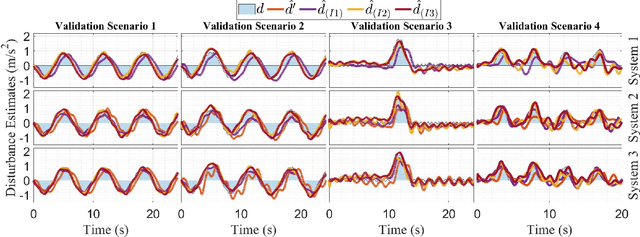
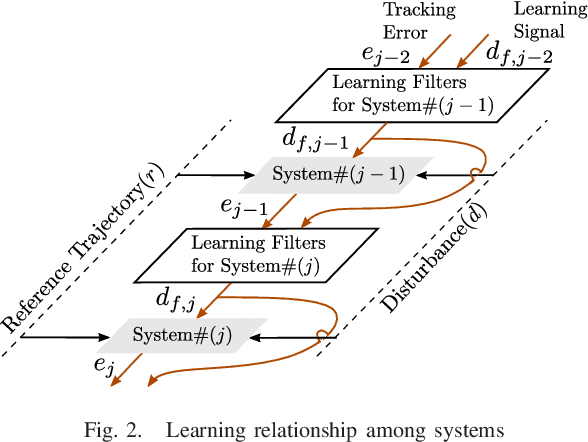
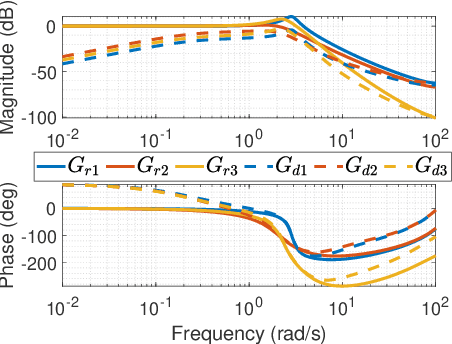
Iterative learning control (ILC) is a method for reducing system tracking or estimation errors over multiple iterations by using information from past iterations. The disturbance observer (DOB) is used to estimate and mitigate disturbances within the system, while the system is being affected by them. ILC enhances system performance by introducing a feedforward signal in each iteration. However, its effectiveness may diminish if the conditions change during the iterations. On the other hand, although DOB effectively mitigates the effects of new disturbances, it cannot entirely eliminate them as it operates reactively. Therefore, neither ILC nor DOB alone can ensure sufficient robustness in challenging scenarios. This study focuses on the simultaneous utilization of ILC and DOB to enhance system robustness. The proposed methodology specifically targets dynamically different linearized systems performing repetitive tasks. The systems share similar forms but differ in dynamics (e.g. sizes, masses, and controllers). Consequently, the design of learning filters must account for these differences in dynamics. To validate the approach, the study establishes a theoretical framework for designing learning filters in conjunction with DOB. The validity of the framework is then confirmed through numerical studies and experimental tests conducted on unmanned aerial vehicles (UAVs). Although UAVs are nonlinear systems, the study employs a linearized controller as they operate in proximity to the hover condition. A video introduction of this paper is available via this link: https://zh.engr.tamu.edu/wp-content/uploads/sites/310/2024/02/ILCDOB_v3f.mp4.