A New K means Grey Wolf Algorithm for Engineering Problems

Purpose: The development of metaheuristic algorithms has increased by researchers to use them extensively in the field of business, science, and engineering. One of the common metaheuristic optimization algorithms is called Grey Wolf Optimization (GWO). The algorithm works based on imitation of the wolves' searching and the process of attacking grey wolves. The main purpose of this paper to overcome the GWO problem which is trapping into local optima. Design or Methodology or Approach: In this paper, the K-means clustering algorithm is used to enhance the performance of the original Grey Wolf Optimization by dividing the population into different parts. The proposed algorithm is called K-means clustering Grey Wolf Optimization (KMGWO). Findings: Results illustrate the efficiency of KMGWO is superior to GWO. To evaluate the performance of the KMGWO, KMGWO applied to solve 10 CEC2019 benchmark test functions. Results prove that KMGWO is better compared to GWO. KMGWO is also compared to Cat Swarm Optimization (CSO), Whale Optimization Algorithm-Bat Algorithm (WOA-BAT), and WOA, so, KMGWO achieves the first rank in terms of performance. Statistical results proved that KMGWO achieved a higher significant value compared to the compared algorithms. Also, the KMGWO is used to solve a pressure vessel design problem and it has outperformed results. Originality/value: Results prove that KMGWO is superior to GWO. KMGWO is also compared to cat swarm optimization (CSO), whale optimization algorithm-bat algorithm (WOA-BAT), WOA, and GWO so KMGWO achieved the first rank in terms of performance. Also, the KMGWO is used to solve a classical engineering problem and it is superior

A Novel Hybrid GWO with WOA for Global Numerical Optimization and Solving Pressure Vessel Design

A recent metaheuristic algorithm, such as Whale Optimization Algorithm (WOA), was proposed. The idea of proposing this algorithm belongs to the hunting behavior of the humpback whale. However, WOA suffers from poor performance in the exploitation phase and stagnates in the local best solution. Grey Wolf Optimization (GWO) is a very competitive algorithm comparing to other common metaheuristic algorithms as it has a super performance in the exploitation phase while it is tested on unimodal benchmark functions. Therefore, the aim of this paper is to hybridize GWO with WOA to overcome the problems. GWO can perform well in exploiting optimal solutions. In this paper, a hybridized WOA with GWO which is called WOAGWO is presented. The proposed hybridized model consists of two steps. Firstly, the hunting mechanism of GWO is embedded into the WOA exploitation phase with a new condition which is related to GWO. Secondly, a new technique is added to the exploration phase to improve the solution after each iteration. Experimentations are tested on three different standard test functions which are called benchmark functions: 23 common functions, 25 CEC2005 functions and 10 CEC2019 functions. The proposed WOAGWO is also evaluated against original WOA, GWO and three other commonly used algorithms. Results show that WOAGWO outperforms other algorithms depending on the Wilcoxon rank-sum test. Finally, WOAGWO is likewise applied to solve an engineering problem such as pressure vessel design. Then the results prove that WOAGWO achieves optimum solution which is better than WOA and Fitness Dependent Optimizer (FDO).

A Systematic and Meta-analysis Survey of Whale Optimization Algorithm

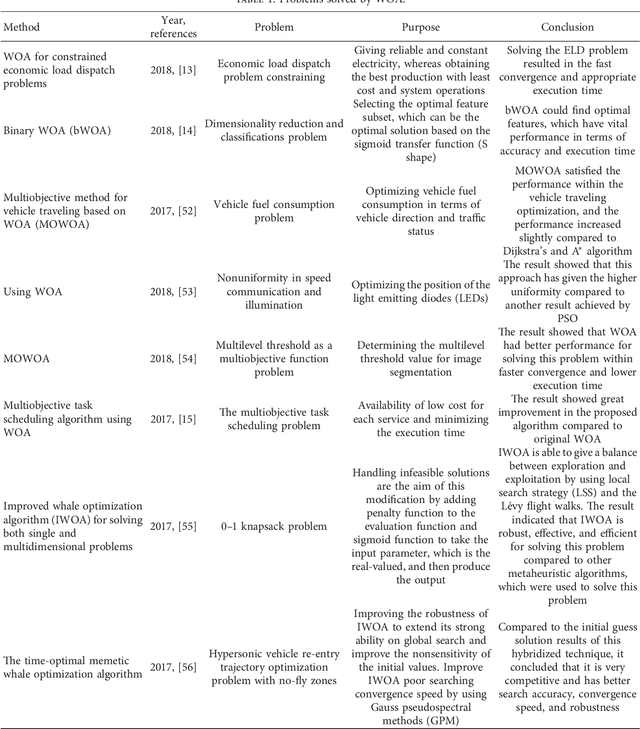
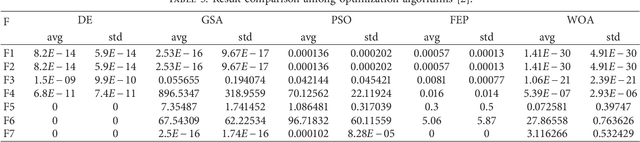
Whale Optimization Algorithm (WOA) is a nature-inspired meta-heuristic optimization algorithm, which was proposed by Mirjalili and Lewis in 2016. This algorithm has shown its ability to solve many problems. Comprehensive surveys have been conducted about some other nature-inspired algorithms, such as ABC, PSO, etc.Nonetheless, no survey search work has been conducted on WOA. Therefore, in this paper, a systematic and meta analysis survey of WOA is conducted to help researchers to use it in different areas or hybridize it with other common algorithms. Thus, WOA is presented in depth in terms of algorithmic backgrounds, its characteristics, limitations, modifications, hybridizations, and applications. Next, WOA performances are presented to solve different problems. Then, the statistical results of WOA modifications and hybridizations are established and compared with the most common optimization algorithms and WOA. The survey's results indicate that WOA performs better than other common algorithms in terms of convergence speed and balancing between exploration and exploitation. WOA modifications and hybridizations also perform well compared to WOA. In addition, our investigation paves a way to present a new technique by hybridizing both WOA and BAT algorithms. The BAT algorithm is used for the exploration phase, whereas the WOA algorithm is used for the exploitation phase. Finally, statistical results obtained from WOA-BAT are very competitive and better than WOA in 16 benchmarks functions. WOA-BAT also outperforms well in 13 functions from CEC2005 and 7 functions from CEC2019.