Functional sufficient dimension reduction through information maximization with application to classification

Considering the case where the response variable is a categorical variable and the predictor is a random function, two novel functional sufficient dimensional reduction (FSDR) methods are proposed based on mutual information and square loss mutual information. Compared to the classical FSDR methods, such as functional sliced inverse regression and functional sliced average variance estimation, the proposed methods are appealing because they are capable of estimating multiple effective dimension reduction directions in the case of a relatively small number of categories, especially for the binary response. Moreover, the proposed methods do not require the restrictive linear conditional mean assumption and the constant covariance assumption. They avoid the inverse problem of the covariance operator which is often encountered in the functional sufficient dimension reduction. The functional principal component analysis with truncation be used as a regularization mechanism. Under some mild conditions, the statistical consistency of the proposed methods is established. It is demonstrated that the two methods are competitive compared with some existing FSDR methods by simulations and real data analyses.

Federated Covariate Shift Adaptation for Missing Target Output Values

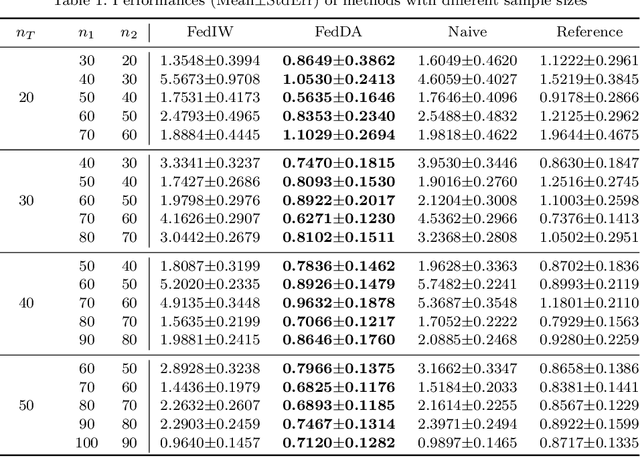
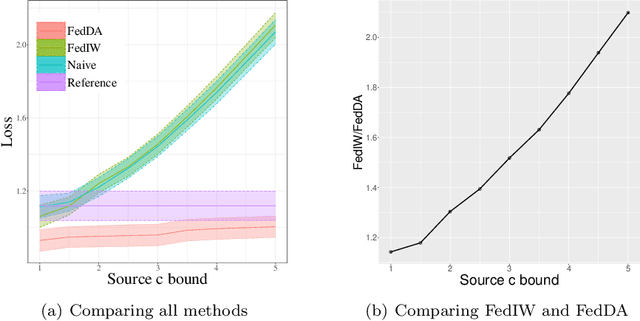
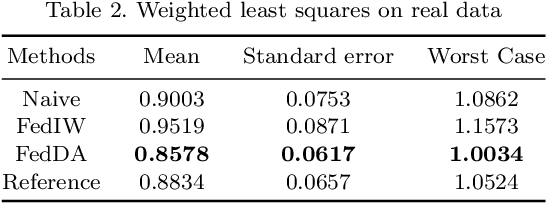
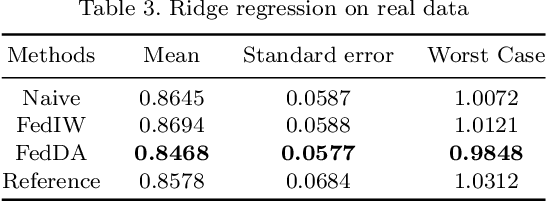
The most recent multi-source covariate shift algorithm is an efficient hyperparameter optimization algorithm for missing target output. In this paper, we extend this algorithm to the framework of federated learning. For data islands in federated learning and covariate shift adaptation, we propose the federated domain adaptation estimate of the target risk which is asymptotically unbiased with a desirable asymptotic variance property. We construct a weighted model for the target task and propose the federated covariate shift adaptation algorithm which works preferably in our setting. The efficacy of our method is justified both theoretically and empirically.

Online Kernel Sliced Inverse Regression

Online dimension reduction is a common method for high-dimensional streaming data processing. Online principal component analysis, online sliced inverse regression, online kernel principal component analysis and other methods have been studied in depth, but as far as we know, online supervised nonlinear dimension reduction methods have not been fully studied. In this article, an online kernel sliced inverse regression method is proposed. By introducing the approximate linear dependence condition and dictionary variable sets, we address the problem of increasing variable dimensions with the sample size in the online kernel sliced inverse regression method, and propose a reduced-order method for updating variables online. We then transform the problem into an online generalized eigen-decomposition problem, and use the stochastic optimization method to update the centered dimension reduction directions. Simulations and the real data analysis show that our method can achieve close performance to batch processing kernel sliced inverse regression.

Federated Sufficient Dimension Reduction Through High-Dimensional Sparse Sliced Inverse Regression

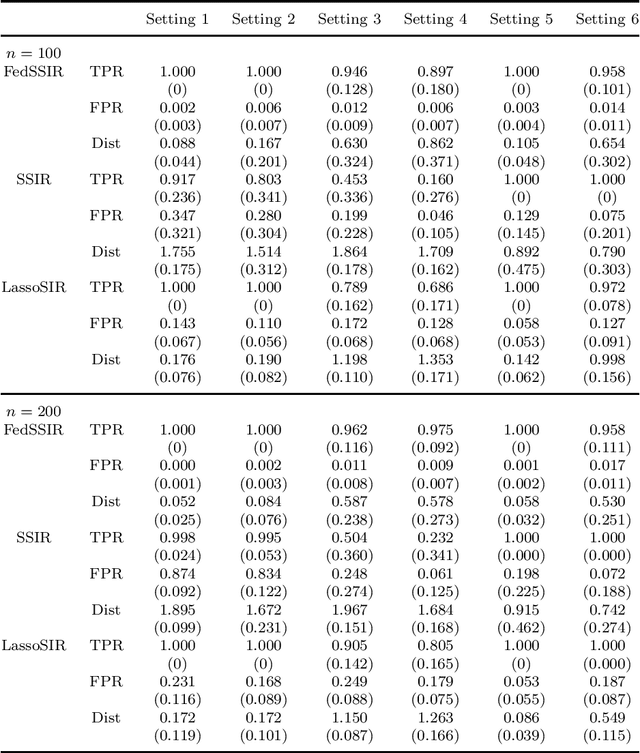
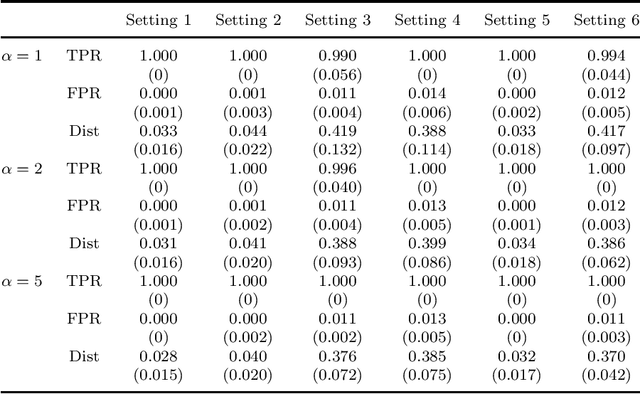
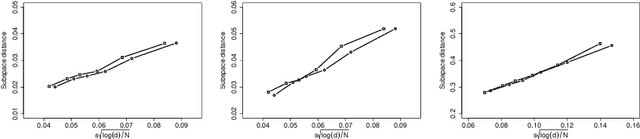
Federated learning has become a popular tool in the big data era nowadays. It trains a centralized model based on data from different clients while keeping data decentralized. In this paper, we propose a federated sparse sliced inverse regression algorithm for the first time. Our method can simultaneously estimate the central dimension reduction subspace and perform variable selection in a federated setting. We transform this federated high-dimensional sparse sliced inverse regression problem into a convex optimization problem by constructing the covariance matrix safely and losslessly. We then use a linearized alternating direction method of multipliers algorithm to estimate the central subspace. We also give approaches of Bayesian information criterion and hold-out validation to ascertain the dimension of the central subspace and the hyper-parameter of the algorithm. We establish an upper bound of the statistical error rate of our estimator under the heterogeneous setting. We demonstrate the effectiveness of our method through simulations and real world applications.