Federated Sufficient Dimension Reduction Through High-Dimensional Sparse Sliced Inverse Regression
Paper and Code
Jan 23, 2023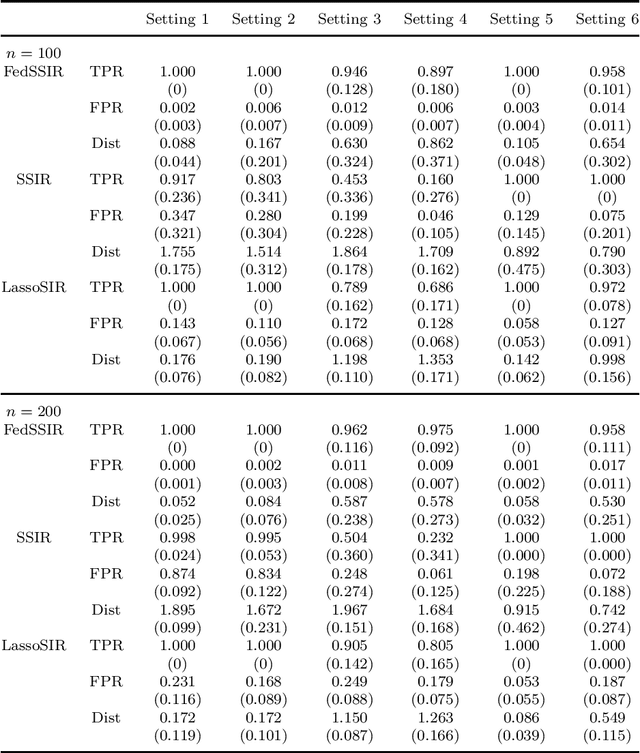
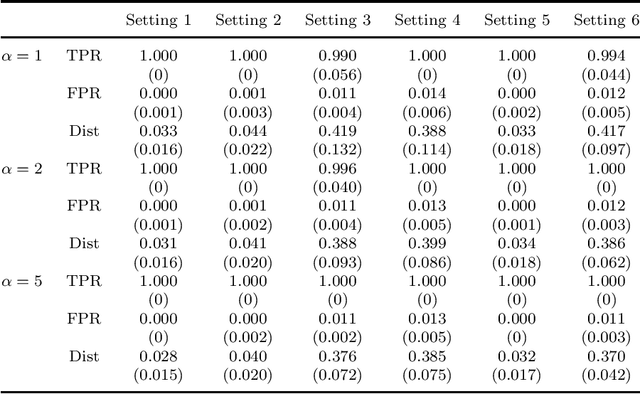
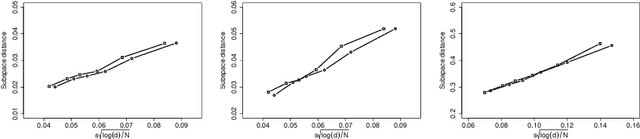

Federated learning has become a popular tool in the big data era nowadays. It trains a centralized model based on data from different clients while keeping data decentralized. In this paper, we propose a federated sparse sliced inverse regression algorithm for the first time. Our method can simultaneously estimate the central dimension reduction subspace and perform variable selection in a federated setting. We transform this federated high-dimensional sparse sliced inverse regression problem into a convex optimization problem by constructing the covariance matrix safely and losslessly. We then use a linearized alternating direction method of multipliers algorithm to estimate the central subspace. We also give approaches of Bayesian information criterion and hold-out validation to ascertain the dimension of the central subspace and the hyper-parameter of the algorithm. We establish an upper bound of the statistical error rate of our estimator under the heterogeneous setting. We demonstrate the effectiveness of our method through simulations and real world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge