Deep Reinforcement Learning for Traveling Purchaser Problems

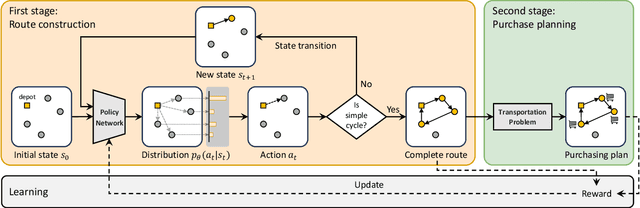
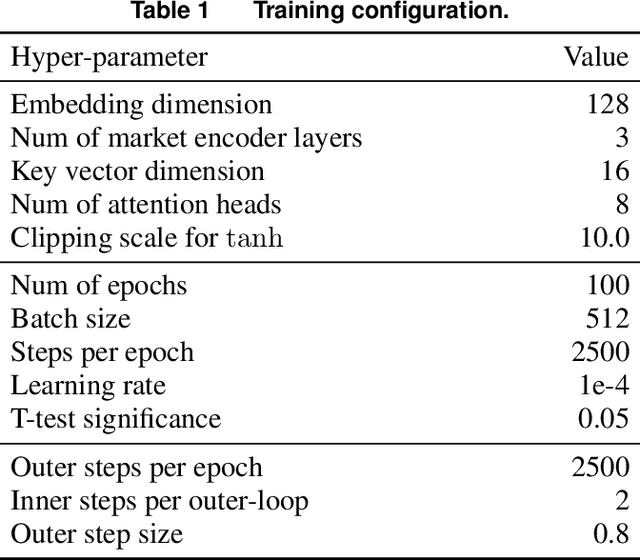
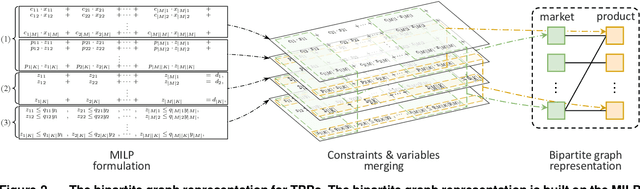
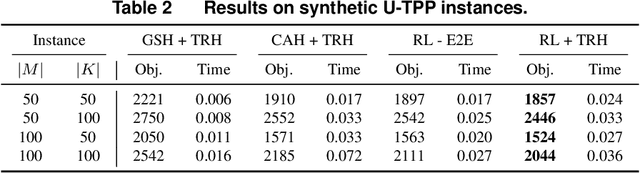
The traveling purchaser problem (TPP) is an important combinatorial optimization problem with broad applications. Due to the coupling between routing and purchasing, existing works on TPPs commonly address route construction and purchase planning simultaneously, which, however, leads to exact methods with high computational cost and heuristics with sophisticated design but limited performance. In sharp contrast, we propose a novel approach based on deep reinforcement learning (DRL), which addresses route construction and purchase planning separately, while evaluating and optimizing the solution from a global perspective. The key components of our approach include a bipartite graph representation for TPPs to capture the market-product relations, and a policy network that extracts information from the bipartite graph and uses it to sequentially construct the route. One significant benefit of our framework is that we can efficiently construct the route using the policy network, and once the route is determined, the associated purchasing plan can be easily derived through linear programming, while, leveraging DRL, we can train the policy network to optimize the global solution objective. Furthermore, by introducing a meta-learning strategy, the policy network can be trained stably on large-sized TPP instances, and generalize well across instances of varying sizes and distributions, even to much larger instances that are never seen during training. Experiments on various synthetic TPP instances and the TPPLIB benchmark demonstrate that our DRL-based approach can significantly outperform well-established TPP heuristics, reducing the optimality gap by 40%-90%, and also showing an advantage in runtime, especially on large-sized instances.

A Reinforcement-Learning-Based Multiple-Column Selection Strategy for Column Generation

Column generation (CG) is one of the most successful approaches for solving large-scale linear programming (LP) problems. Given an LP with a prohibitively large number of variables (i.e., columns), the idea of CG is to explicitly consider only a subset of columns and iteratively add potential columns to improve the objective value. While adding the column with the most negative reduced cost can guarantee the convergence of CG, it has been shown that adding multiple columns per iteration rather than a single column can lead to faster convergence. However, it remains a challenge to design a multiple-column selection strategy to select the most promising columns from a large number of candidate columns. In this paper, we propose a novel reinforcement-learning-based (RL) multiple-column selection strategy. To the best of our knowledge, it is the first RL-based multiple-column selection strategy for CG. The effectiveness of our approach is evaluated on two sets of problems: the cutting stock problem and the graph coloring problem. Compared to several widely used single-column and multiple-column selection strategies, our RL-based multiple-column selection strategy leads to faster convergence and achieves remarkable reductions in the number of CG iterations and runtime.

The Neural-Prediction based Acceleration Algorithm of Column Generation for Graph-Based Set Covering Problems

Set covering problem is an important class of combinatorial optimization problems, which has been widely applied and studied in many fields. In this paper, we propose an improved column generation algorithm with neural prediction (CG-P) for solving graph-based set covering problems. We leverage a graph neural network based neural prediction model to predict the probability to be included in the final solution for each edge. Our CG-P algorithm constructs a reduced graph that only contains the edges with higher predicted probability, and this graph reduction process significantly speeds up the solution process. We evaluate the CG-P algorithm on railway crew scheduling problems and it outperforms the baseline column generation algorithm. We provide two solution modes for our CG-P algorithm. In the optimal mode, we can obtain a solution with an optimality guarantee while reducing the time cost to 63.12%. In the fast mode, we can obtain a sub-optimal solution with a 7.62% optimality gap in only 2.91% computation time.