Matrix Sketching in Bandits: Current Pitfalls and New Framework

The utilization of sketching techniques has progressively emerged as a pivotal method for enhancing the efficiency of online learning. In linear bandit settings, current sketch-based approaches leverage matrix sketching to reduce the per-round time complexity from \(\Omega\left(d^2\right)\) to \(O(d)\), where \(d\) is the input dimension. Despite this improved efficiency, these approaches encounter critical pitfalls: if the spectral tail of the covariance matrix does not decrease rapidly, it can lead to linear regret. In this paper, we revisit the regret analysis and algorithm design concerning approximating the covariance matrix using matrix sketching in linear bandits. We illustrate how inappropriate sketch sizes can result in unbounded spectral loss, thereby causing linear regret. To prevent this issue, we propose Dyadic Block Sketching, an innovative streaming matrix sketching approach that adaptively manages sketch size to constrain global spectral loss. This approach effectively tracks the best rank-\( k \) approximation in an online manner, ensuring efficiency when the geometry of the covariance matrix is favorable. Then, we apply the proposed Dyadic Block Sketching to linear bandits and demonstrate that the resulting bandit algorithm can achieve sublinear regret without prior knowledge of the covariance matrix, even under the worst case. Our method is a general framework for efficient sketch-based linear bandits, applicable to all existing sketch-based approaches, and offers improved regret bounds accordingly. Additionally, we conduct comprehensive empirical studies using both synthetic and real-world data to validate the accuracy of our theoretical findings and to highlight the effectiveness of our algorithm.

Optimal Matrix Sketching over Sliding Windows

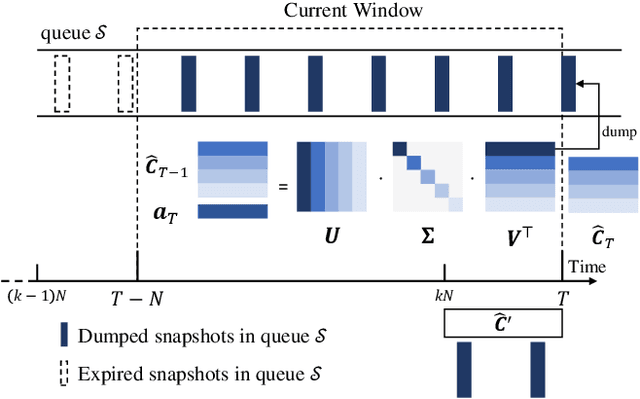
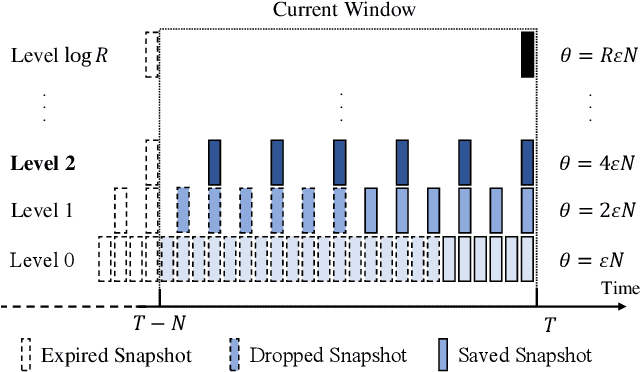
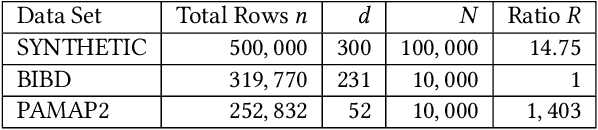
Matrix sketching, aimed at approximating a matrix $\boldsymbol{A} \in \mathbb{R}^{N\times d}$ consisting of vector streams of length $N$ with a smaller sketching matrix $\boldsymbol{B} \in \mathbb{R}^{\ell\times d}, \ell \ll N$, has garnered increasing attention in fields such as large-scale data analytics and machine learning. A well-known deterministic matrix sketching method is the Frequent Directions algorithm, which achieves the optimal $O\left(\frac{d}{\varepsilon}\right)$ space bound and provides a covariance error guarantee of $\varepsilon = \lVert \boldsymbol{A}^\top \boldsymbol{A} - \boldsymbol{B}^\top \boldsymbol{B} \rVert_2/\lVert \boldsymbol{A} \rVert_F^2$. The matrix sketching problem becomes particularly interesting in the context of sliding windows, where the goal is to approximate the matrix $\boldsymbol{A}_W$, formed by input vectors over the most recent $N$ time units. However, despite recent efforts, whether achieving the optimal $O\left(\frac{d}{\varepsilon}\right)$ space bound on sliding windows is possible has remained an open question. In this paper, we introduce the DS-FD algorithm, which achieves the optimal $O\left(\frac{d}{\varepsilon}\right)$ space bound for matrix sketching over row-normalized, sequence-based sliding windows. We also present matching upper and lower space bounds for time-based and unnormalized sliding windows, demonstrating the generality and optimality of \dsfd across various sliding window models. This conclusively answers the open question regarding the optimal space bound for matrix sketching over sliding windows. Furthermore, we conduct extensive experiments with both synthetic and real-world datasets, validating our theoretical claims and thus confirming the correctness and effectiveness of our algorithm, both theoretically and empirically.