Federated scientific machine learning for approximating functions and solving differential equations with data heterogeneity

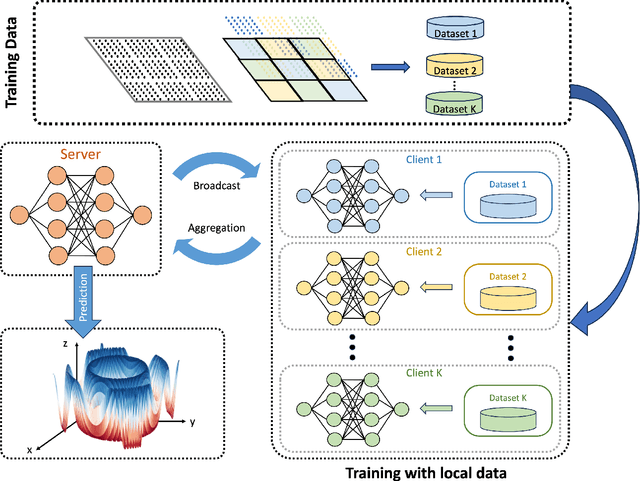
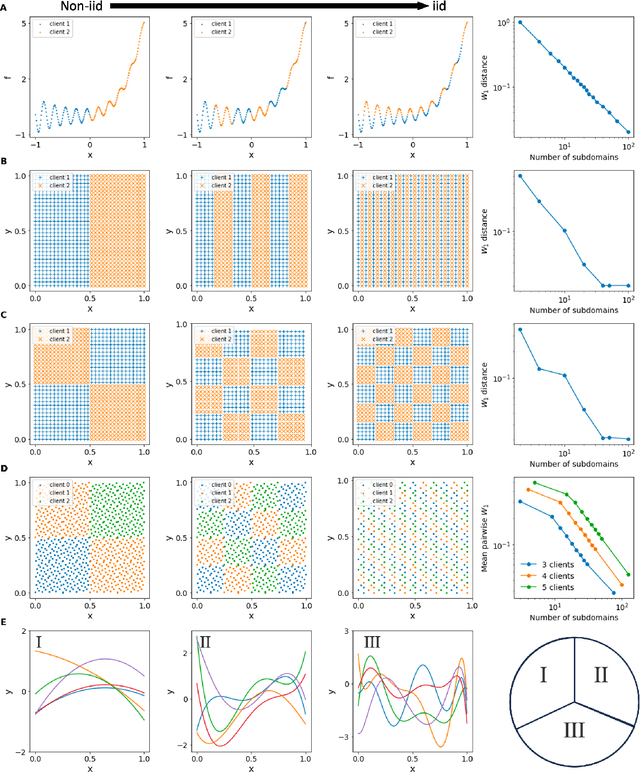
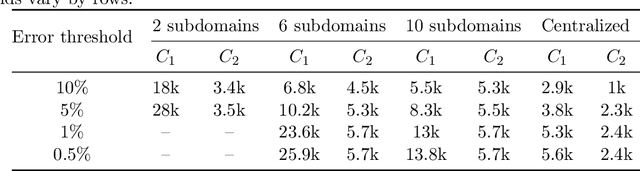
By leveraging neural networks, the emerging field of scientific machine learning (SciML) offers novel approaches to address complex problems governed by partial differential equations (PDEs). In practical applications, challenges arise due to the distributed essence of data, concerns about data privacy, or the impracticality of transferring large volumes of data. Federated learning (FL), a decentralized framework that enables the collaborative training of a global model while preserving data privacy, offers a solution to the challenges posed by isolated data pools and sensitive data issues. Here, this paper explores the integration of FL and SciML to approximate complex functions and solve differential equations. We propose two novel models: federated physics-informed neural networks (FedPINN) and federated deep operator networks (FedDeepONet). We further introduce various data generation methods to control the degree of non-independent and identically distributed (non-iid) data and utilize the 1-Wasserstein distance to quantify data heterogeneity in function approximation and PDE learning. We systematically investigate the relationship between data heterogeneity and federated model performance. Additionally, we propose a measure of weight divergence and develop a theoretical framework to establish growth bounds for weight divergence in federated learning compared to traditional centralized learning. To demonstrate the effectiveness of our methods, we conducted 10 experiments, including 2 on function approximation, 5 PDE problems on FedPINN, and 3 PDE problems on FedDeepONet. These experiments demonstrate that proposed federated methods surpass the models trained only using local data and achieve competitive accuracy of centralized models trained using all data.

Reliable extrapolation of deep neural operators informed by physics or sparse observations

Deep neural operators can learn nonlinear mappings between infinite-dimensional function spaces via deep neural networks. As promising surrogate solvers of partial differential equations (PDEs) for real-time prediction, deep neural operators such as deep operator networks (DeepONets) provide a new simulation paradigm in science and engineering. Pure data-driven neural operators and deep learning models, in general, are usually limited to interpolation scenarios, where new predictions utilize inputs within the support of the training set. However, in the inference stage of real-world applications, the input may lie outside the support, i.e., extrapolation is required, which may result to large errors and unavoidable failure of deep learning models. Here, we address this challenge of extrapolation for deep neural operators. First, we systematically investigate the extrapolation behavior of DeepONets by quantifying the extrapolation complexity via the 2-Wasserstein distance between two function spaces and propose a new behavior of bias-variance trade-off for extrapolation with respect to model capacity. Subsequently, we develop a complete workflow, including extrapolation determination, and we propose five reliable learning methods that guarantee a safe prediction under extrapolation by requiring additional information -- the governing PDEs of the system or sparse new observations. The proposed methods are based on either fine-tuning a pre-trained DeepONet or multifidelity learning. We demonstrate the effectiveness of the proposed framework for various types of parametric PDEs. Our systematic comparisons provide practical guidelines for selecting a proper extrapolation method depending on the available information, desired accuracy, and required inference speed.