Federated scientific machine learning for approximating functions and solving differential equations with data heterogeneity
Paper and Code
Oct 17, 2024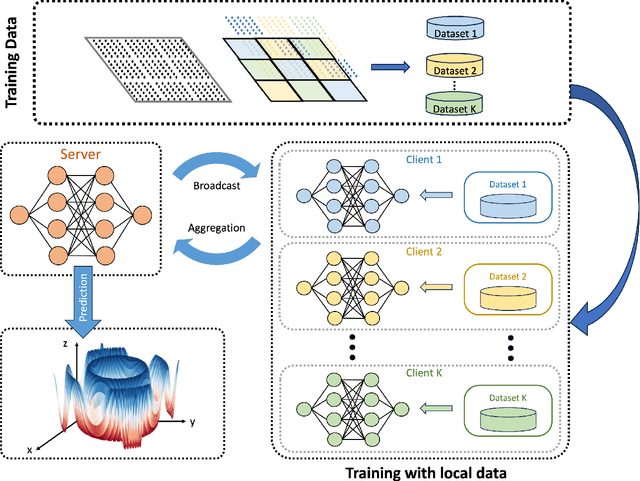

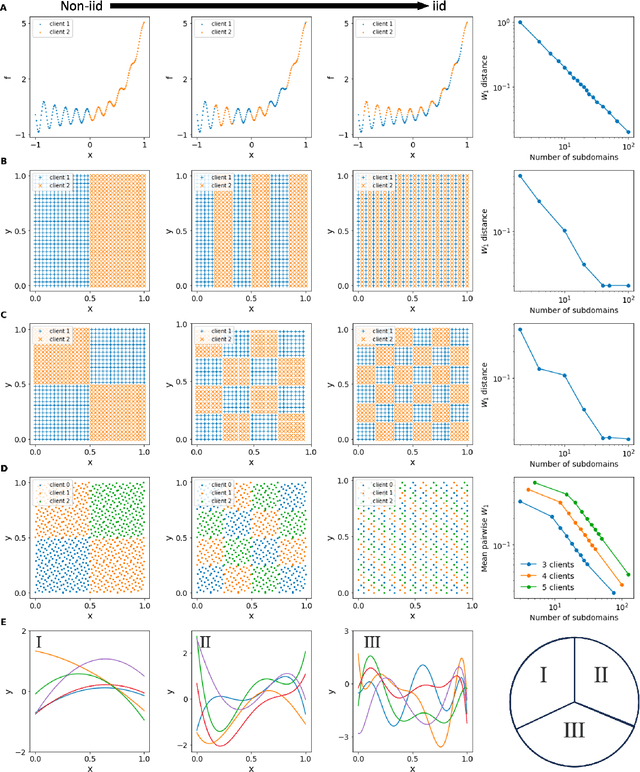
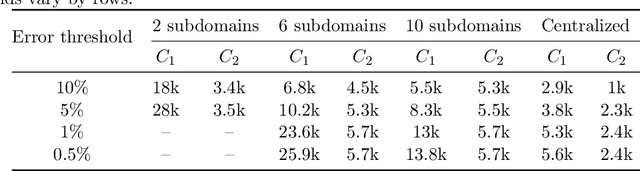
By leveraging neural networks, the emerging field of scientific machine learning (SciML) offers novel approaches to address complex problems governed by partial differential equations (PDEs). In practical applications, challenges arise due to the distributed essence of data, concerns about data privacy, or the impracticality of transferring large volumes of data. Federated learning (FL), a decentralized framework that enables the collaborative training of a global model while preserving data privacy, offers a solution to the challenges posed by isolated data pools and sensitive data issues. Here, this paper explores the integration of FL and SciML to approximate complex functions and solve differential equations. We propose two novel models: federated physics-informed neural networks (FedPINN) and federated deep operator networks (FedDeepONet). We further introduce various data generation methods to control the degree of non-independent and identically distributed (non-iid) data and utilize the 1-Wasserstein distance to quantify data heterogeneity in function approximation and PDE learning. We systematically investigate the relationship between data heterogeneity and federated model performance. Additionally, we propose a measure of weight divergence and develop a theoretical framework to establish growth bounds for weight divergence in federated learning compared to traditional centralized learning. To demonstrate the effectiveness of our methods, we conducted 10 experiments, including 2 on function approximation, 5 PDE problems on FedPINN, and 3 PDE problems on FedDeepONet. These experiments demonstrate that proposed federated methods surpass the models trained only using local data and achieve competitive accuracy of centralized models trained using all data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge