Sampling-based sublinear low-rank matrix arithmetic framework for dequantizing quantum machine learning

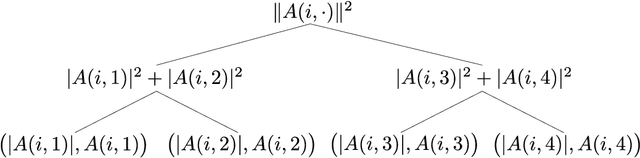
We present an algorithmic framework generalizing quantum-inspired polylogarithmic-time algorithms on low-rank matrices. Our work follows the line of research started by Tang's breakthrough classical algorithm for recommendation systems [STOC'19]. The main result of this work is an algorithm for singular value transformation on low-rank inputs in the quantum-inspired regime, where singular value transformation is a framework proposed by Gily\'en et al. [STOC'19] to study various quantum speedups. Since singular value transformation encompasses a vast range of matrix arithmetic, this result, combined with simple sampling lemmas from previous work, suffices to generalize all results dequantizing quantum machine learning algorithms to the authors' knowledge. Via simple black-box applications of our singular value transformation framework, we recover the dequantization results on recommendation systems, principal component analysis, supervised clustering, low-rank matrix inversion, low-rank semidefinite programming, and support vector machines. We also give additional dequantizations results on low-rank Hamiltonian simulation and discriminant analysis.

Quantum-inspired classical sublinear-time algorithm for solving low-rank semidefinite programming via sampling approaches

Semidefinite programming (SDP) is a central topic in mathematical optimization with extensive studies on its efficient solvers. Recently, quantum algorithms with superpolynomial speedups for solving SDPs have been proposed assuming access to its constraint matrices in quantum superposition. Mutually inspired by both classical and quantum SDP solvers, in this paper we present a sublinear classical algorithm for solving low-rank SDPs which is asymptotically as good as existing quantum algorithms. Specifically, given an SDP with $m$ constraint matrices, each of dimension $n$ and rank $\mathrm{poly}(\log n)$, our algorithm gives a succinct description and any entry of the solution matrix in time $O(m\cdot\mathrm{poly}(\log n,1/\varepsilon))$ given access to a sample-based low-overhead data structure of the constraint matrices, where $\varepsilon$ is the precision of the solution. In addition, we apply our algorithm to a quantum state learning task as an application. Technically, our approach aligns with both the SDP solvers based on the matrix multiplicative weight (MMW) framework and the recent studies of quantum-inspired machine learning algorithms. The cost of solving SDPs by MMW mainly comes from the exponentiation of Hermitian matrices, and we propose two new technical ingredients (compared to previous sample-based algorithms) for this task that may be of independent interest: $\bullet$ Weighted sampling: assuming sampling access to each individual constraint matrix $A_{1},\ldots,A_{\tau}$, we propose a procedure that gives a good approximation of $A=A_{1}+\cdots+A_{\tau}$. $\bullet$ Symmetric approximation: we propose a sampling procedure that gives low-rank spectral decomposition of a Hermitian matrix $A$. This improves upon previous sampling procedures that only give low-rank singular value decompositions, losing the signs of eigenvalues.

Quantum-inspired sublinear classical algorithms for solving low-rank linear systems

We present classical sublinear-time algorithms for solving low-rank linear systems of equations. Our algorithms are inspired by the HHL quantum algorithm for solving linear systems and the recent breakthrough by Tang of dequantizing the quantum algorithm for recommendation systems. Let $A \in \mathbb{C}^{m \times n}$ be a rank-$k$ matrix, and $b \in \mathbb{C}^m$ be a vector. We present two algorithms: a "sampling" algorithm that provides a sample from $A^{-1}b$ and a "query" algorithm that outputs an estimate of an entry of $A^{-1}b$, where $A^{-1}$ denotes the Moore-Penrose pseudo-inverse. Both of our algorithms have query and time complexity $O(\mathrm{poly}(k, \kappa, \|A\|_F, 1/\epsilon)\,\mathrm{polylog}(m, n))$, where $\kappa$ is the condition number of $A$ and $\epsilon$ is the precision parameter. Note that the algorithms we consider are sublinear time, so they cannot write and read the whole matrix or vectors. In this paper, we assume that $A$ and $b$ come with well-known low-overhead data structures such that entries of $A$ and $b$ can be sampled according to some natural probability distributions. Alternatively, when $A$ is positive semidefinite, our algorithms can be adapted so that the sampling assumption on $b$ is not required.

On the Sample Complexity of PAC Learning Quantum Process

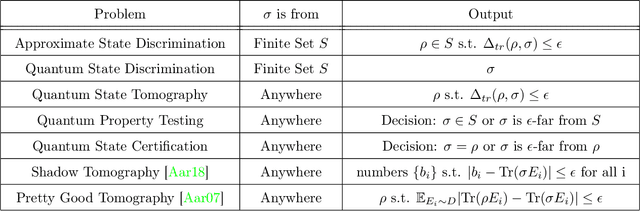
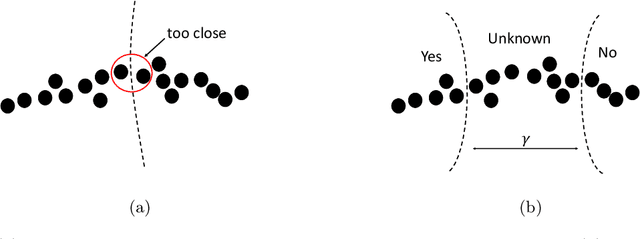
We generalize the PAC (probably approximately correct) learning model to the quantum world by generalizing the concepts from classical functions to quantum processes, defining the problem of \emph{PAC learning quantum process}, and study its sample complexity. In the problem of PAC learning quantum process, we want to learn an $\epsilon$-approximate of an unknown quantum process $c^*$ from a known finite concept class $C$ with probability $1-\delta$ using samples $\{(x_1,c^*(x_1)),(x_2,c^*(x_2)),\dots\}$, where $\{x_1,x_2, \dots\}$ are computational basis states sampled from an unknown distribution $D$ and $\{c^*(x_1),c^*(x_2),\dots\}$ are the (possibly mixed) quantum states outputted by $c^*$. The special case of PAC-learning quantum process under constant input reduces to a natural problem which we named as approximate state discrimination, where we are given copies of an unknown quantum state $c^*$ from an known finite set $C$, and we want to learn with probability $1-\delta$ an $\epsilon$-approximate of $c^*$ with as few copies of $c^*$ as possible. We show that the problem of PAC learning quantum process can be solved with $$O\left(\frac{\log|C| + \log(1/ \delta)} { \epsilon^2}\right)$$ samples when the outputs are pure states and $$O\left(\frac{\log^3 |C|(\log |C|+\log(1/ \delta))} { \epsilon^2}\right)$$ samples if the outputs can be mixed. Some implications of our results are that we can PAC-learn a polynomial sized quantum circuit in polynomial samples and approximate state discrimination can be solved in polynomial samples even when concept class size $|C|$ is exponential in the number of qubits, an exponentially improvement over a full state tomography.