Statistical Inference of Optimal Allocations I: Regularities and their Implications

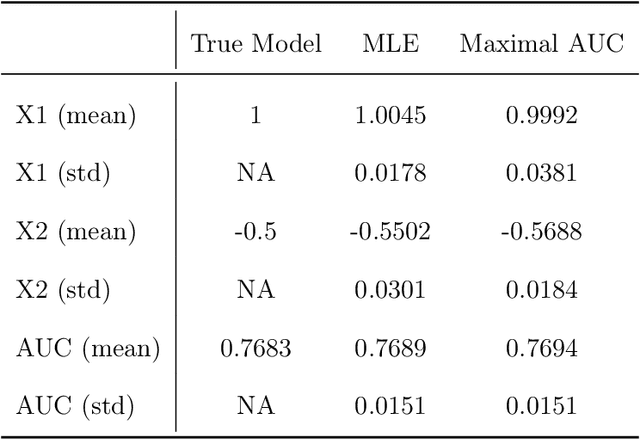
In this paper, we develop a functional differentiability approach for solving statistical optimal allocation problems. We first derive Hadamard differentiability of the value function through a detailed analysis of the general properties of the sorting operator. Central to our framework are the concept of Hausdorff measure and the area and coarea integration formulas from geometric measure theory. Building on our Hadamard differentiability results, we demonstrate how the functional delta method can be used to directly derive the asymptotic properties of the value function process for binary constrained optimal allocation problems, as well as the two-step ROC curve estimator. Moreover, leveraging profound insights from geometric functional analysis on convex and local Lipschitz functionals, we obtain additional generic Fr\'echet differentiability results for the value functions of optimal allocation problems. These compelling findings motivate us to study carefully the first order approximation of the optimal social welfare. In this paper, we then present a double / debiased estimator for the value functions. Importantly, the conditions outlined in the Hadamard differentiability section validate the margin assumption from the statistical classification literature employing plug-in methods that justifies a faster convergence rate.

Statistical Tests for Replacing Human Decision Makers with Algorithms

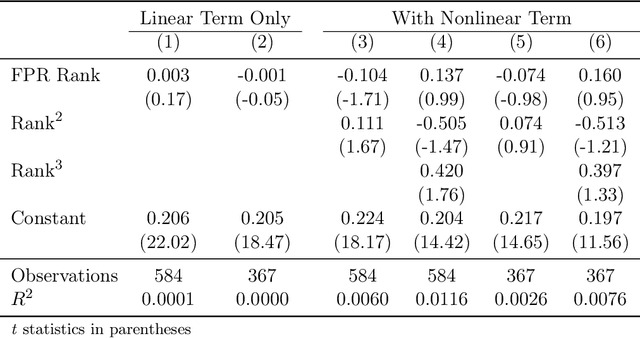
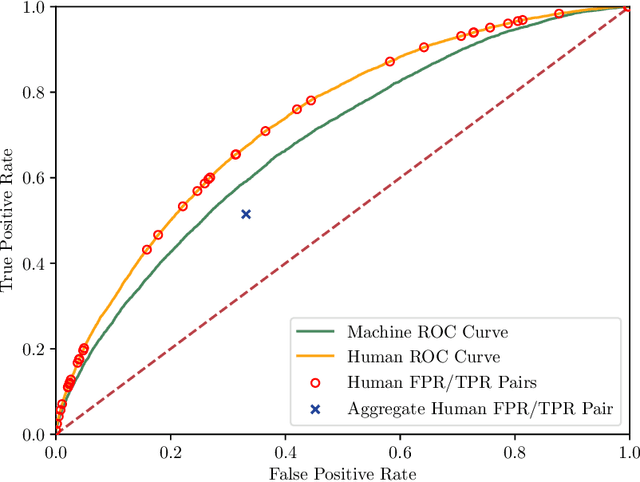
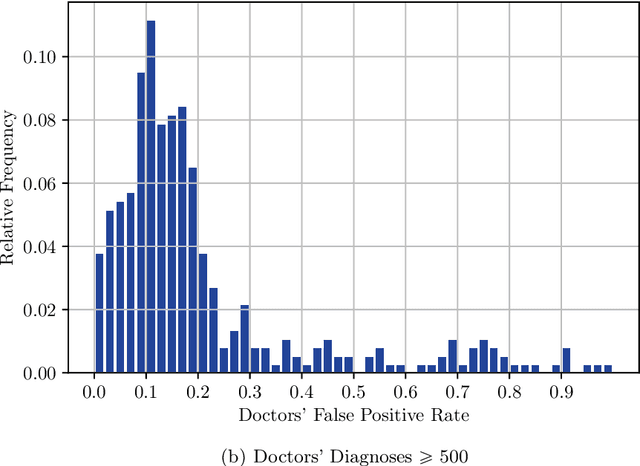
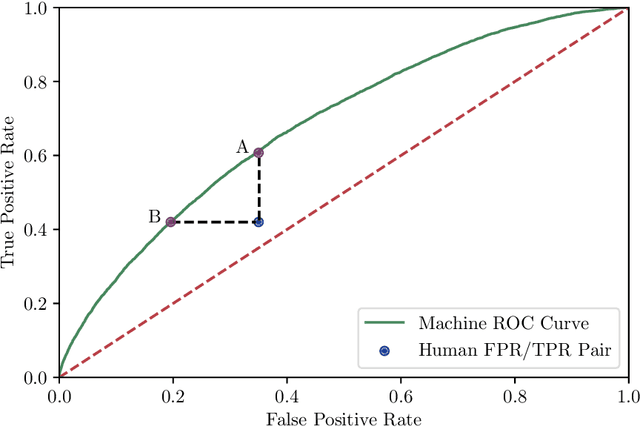
This paper proposes a statistical framework with which artificial intelligence can improve human decision making. The performance of each human decision maker is first benchmarked against machine predictions; we then replace the decisions made by a subset of the decision makers with the recommendation from the proposed artificial intelligence algorithm. Using a large nationwide dataset of pregnancy outcomes and doctor diagnoses from prepregnancy checkups of reproductive age couples, we experimented with both a heuristic frequentist approach and a Bayesian posterior loss function approach with an application to abnormal birth detection. We find that our algorithm on a test dataset results in a higher overall true positive rate and a lower false positive rate than the diagnoses made by doctors only. We also find that the diagnoses of doctors from rural areas are more frequently replaceable, suggesting that artificial intelligence assisted decision making tends to improve precision more in less developed regions.

Decision Making with Machine Learning and ROC Curves

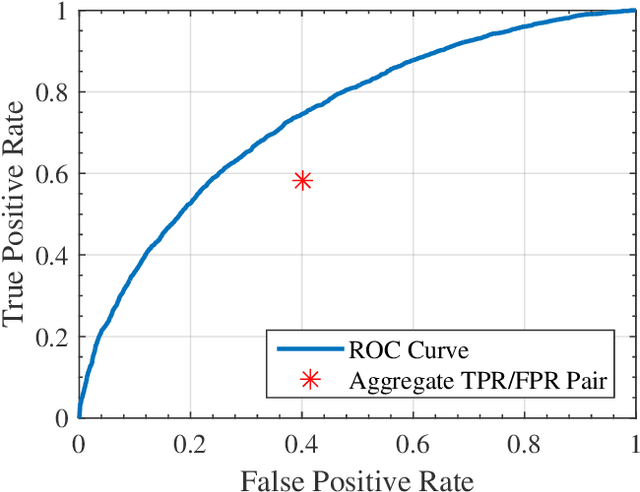
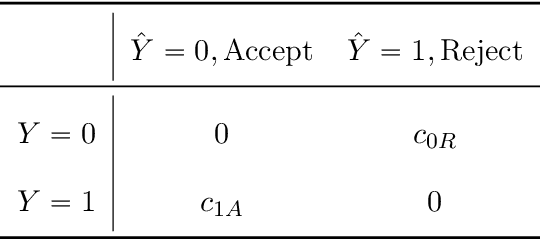
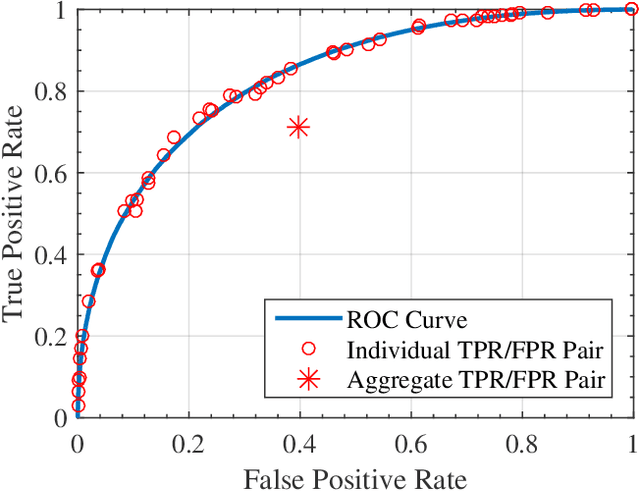
The Receiver Operating Characteristic (ROC) curve is a representation of the statistical information discovered in binary classification problems and is a key concept in machine learning and data science. This paper studies the statistical properties of ROC curves and its implication on model selection. We analyze the implications of different models of incentive heterogeneity and information asymmetry on the relation between human decisions and the ROC curves. Our theoretical discussion is illustrated in the context of a large data set of pregnancy outcomes and doctor diagnosis from the Pre-Pregnancy Checkups of reproductive age couples in Henan Province provided by the Chinese Ministry of Health.