Evidential Uncertainty Sets in Deep Classifiers Using Conformal Prediction

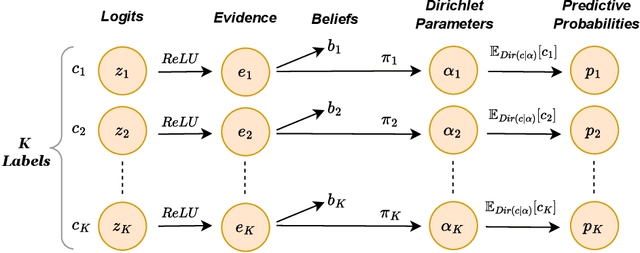
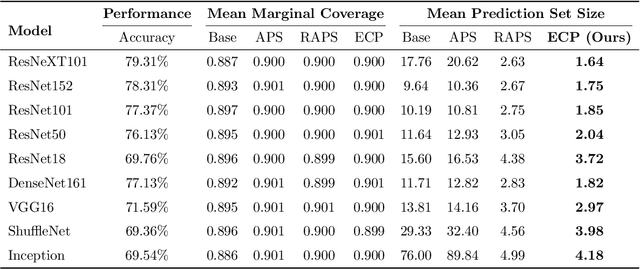
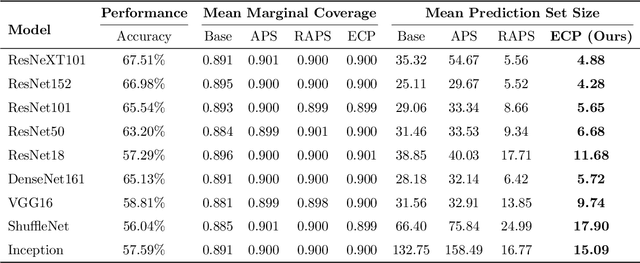
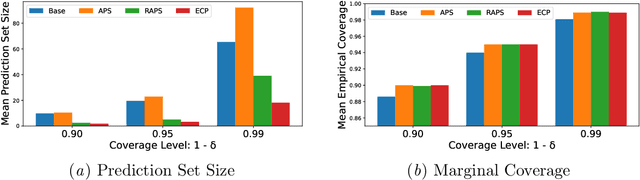
In this paper, we propose Evidential Conformal Prediction (ECP) method for image classifiers to generate the conformal prediction sets. Our method is designed based on a non-conformity score function that has its roots in Evidential Deep Learning (EDL) as a method of quantifying model (epistemic) uncertainty in DNN classifiers. We use evidence that are derived from the logit values of target labels to compute the components of our non-conformity score function: the heuristic notion of uncertainty in CP, uncertainty surprisal, and expected utility. Our extensive experimental evaluation demonstrates that ECP outperforms three state-of-the-art methods for generating CP sets, in terms of their set sizes and adaptivity while maintaining the coverage of true labels.

Quantifying Deep Learning Model Uncertainty in Conformal Prediction

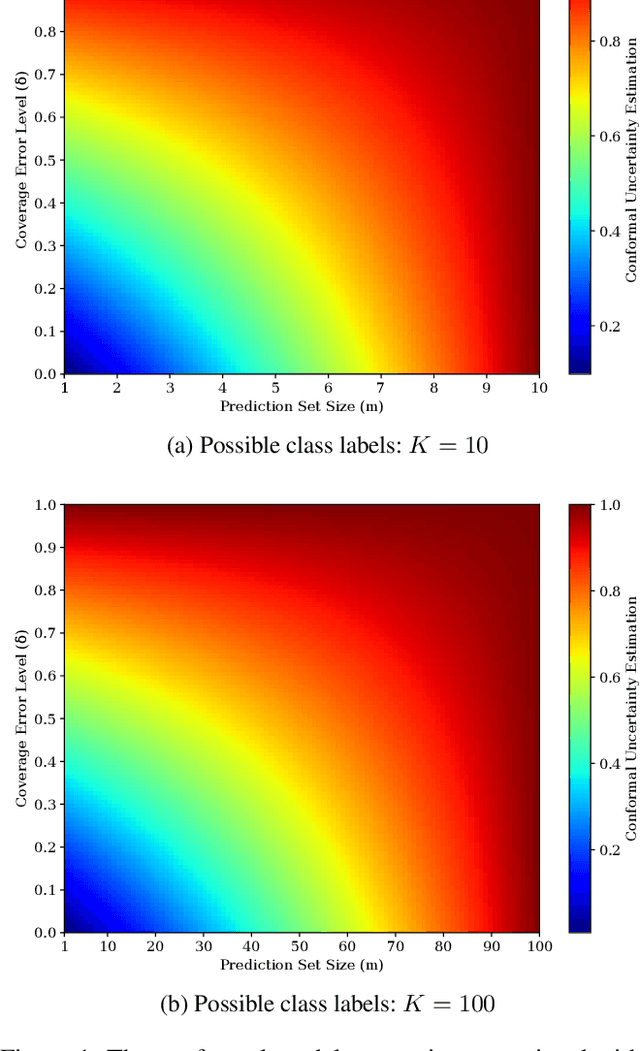
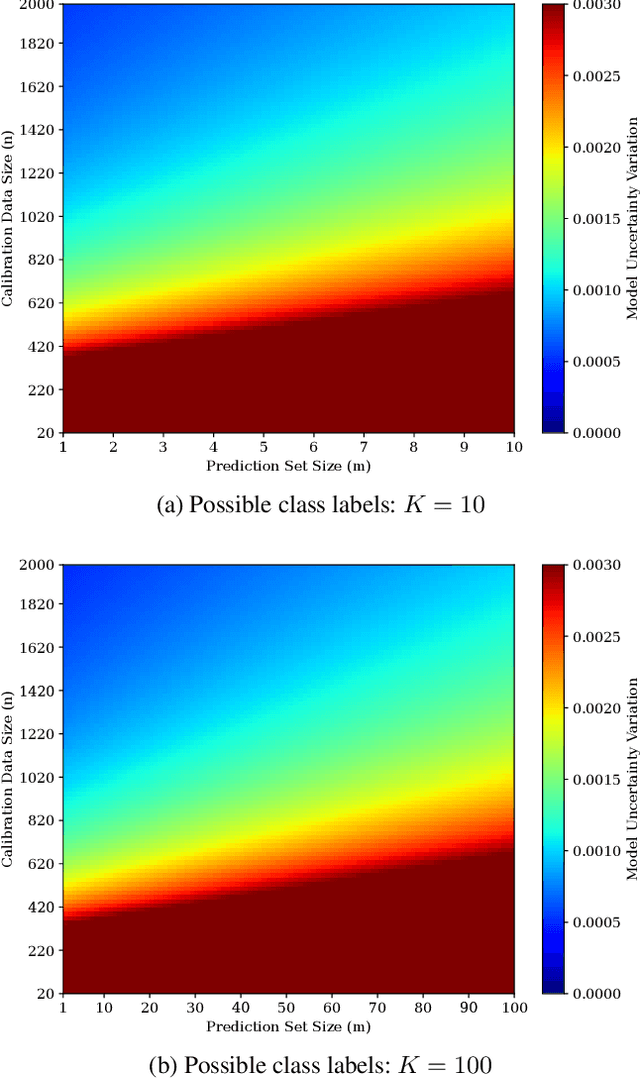
Precise estimation of predictive uncertainty in deep neural networks is a critical requirement for reliable decision-making in machine learning and statistical modeling, particularly in the context of medical AI. Conformal Prediction (CP) has emerged as a promising framework for representing the model uncertainty by providing well-calibrated confidence levels for individual predictions. However, the quantification of model uncertainty in conformal prediction remains an active research area, yet to be fully addressed. In this paper, we explore state-of-the-art CP methodologies and their theoretical foundations. We propose a probabilistic approach in quantifying the model uncertainty derived from the produced prediction sets in conformal prediction and provide certified boundaries for the computed uncertainty. By doing so, we allow model uncertainty measured by CP to be compared by other uncertainty quantification methods such as Bayesian (e.g., MC-Dropout and DeepEnsemble) and Evidential approaches.

Linear Convergence of Gradient and Proximal-Gradient Methods Under the Polyak-Łojasiewicz Condition

In 1963, Polyak proposed a simple condition that is sufficient to show a global linear convergence rate for gradient descent. This condition is a special case of the \L{}ojasiewicz inequality proposed in the same year, and it does not require strong convexity (or even convexity). In this work, we show that this much-older Polyak-\L{}ojasiewicz (PL) inequality is actually weaker than the main conditions that have been explored to show linear convergence rates without strong convexity over the last 25 years. We also use the PL inequality to give new analyses of randomized and greedy coordinate descent methods, sign-based gradient descent methods, and stochastic gradient methods in the classic setting (with decreasing or constant step-sizes) as well as the variance-reduced setting. We further propose a generalization that applies to proximal-gradient methods for non-smooth optimization, leading to simple proofs of linear convergence of these methods. Along the way, we give simple convergence results for a wide variety of problems in machine learning: least squares, logistic regression, boosting, resilient backpropagation, L1-regularization, support vector machines, stochastic dual coordinate ascent, and stochastic variance-reduced gradient methods.