Modeling Inverse Demand Function with Explainable Dual Neural Networks

Financial contagion has been widely recognized as a fundamental risk to the financial system. Particularly potent is price-mediated contagion, wherein forced liquidations by firms depress asset prices and propagate financial stress, enabling crises to proliferate across a broad spectrum of seemingly unrelated entities. Price impacts are currently modeled via exogenous inverse demand functions. However, in real-world scenarios, only the initial shocks and the final equilibrium asset prices are typically observable, leaving actual asset liquidations largely obscured. This missing data presents significant limitations to calibrating the existing models. To address these challenges, we introduce a novel dual neural network structure that operates in two sequential stages: the first neural network maps initial shocks to predicted asset liquidations, and the second network utilizes these liquidations to derive resultant equilibrium prices. This data-driven approach can capture both linear and non-linear forms without pre-specifying an analytical structure; furthermore, it functions effectively even in the absence of observable liquidation data. Experiments with simulated datasets demonstrate that our model can accurately predict equilibrium asset prices based solely on initial shocks, while revealing a strong alignment between predicted and true liquidations. Our explainable framework contributes to the understanding and modeling of price-mediated contagion and provides valuable insights for financial authorities to construct effective stress tests and regulatory policies.

Optimal Network Compression

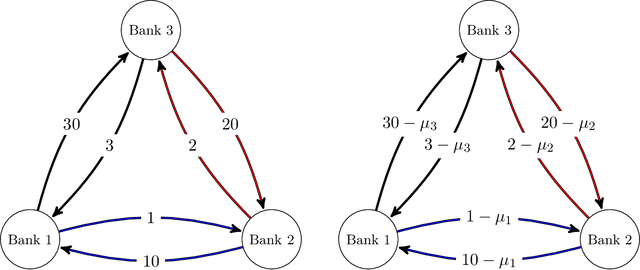
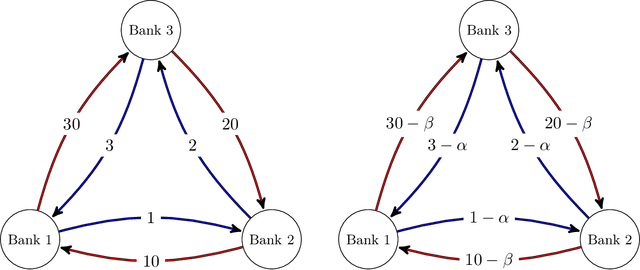
This paper introduces a formulation of the optimal network compression problem for financial systems. This general formulation is presented for different levels of network compression or rerouting allowed from the initial interbank network. We prove that this problem is, generically, NP-hard. We focus on objective functions generated by systemic risk measures under systematic shocks to the financial network. We conclude by studying the optimal compression problem for specific networks; this permits us to study the so-called robust fragility of certain network topologies more generally as well as the potential benefits and costs of network compression.

Including Physics in Deep Learning -- An example from 4D seismic pressure saturation inversion

Geoscience data often have to rely on strong priors in the face of uncertainty. Additionally, we often try to detect or model anomalous sparse data that can appear as an outlier in machine learning models. These are classic examples of imbalanced learning. Approaching these problems can benefit from including prior information from physics models or transforming data to a beneficial domain. We show an example of including physical information in the architecture of a neural network as prior information. We go on to present noise injection at training time to successfully transfer the network from synthetic data to field data.