Haixia Jia
From spin glasses to hard satisfiable formulas
Oct 17, 2012
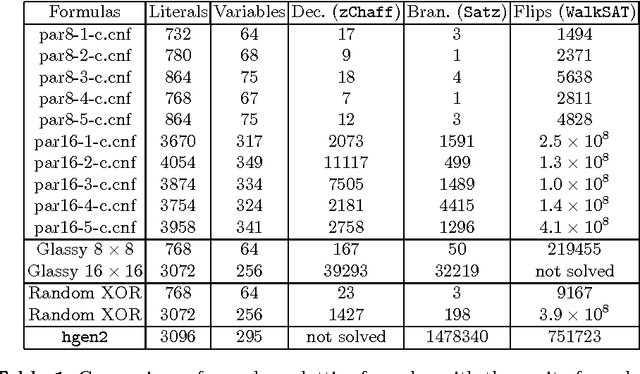
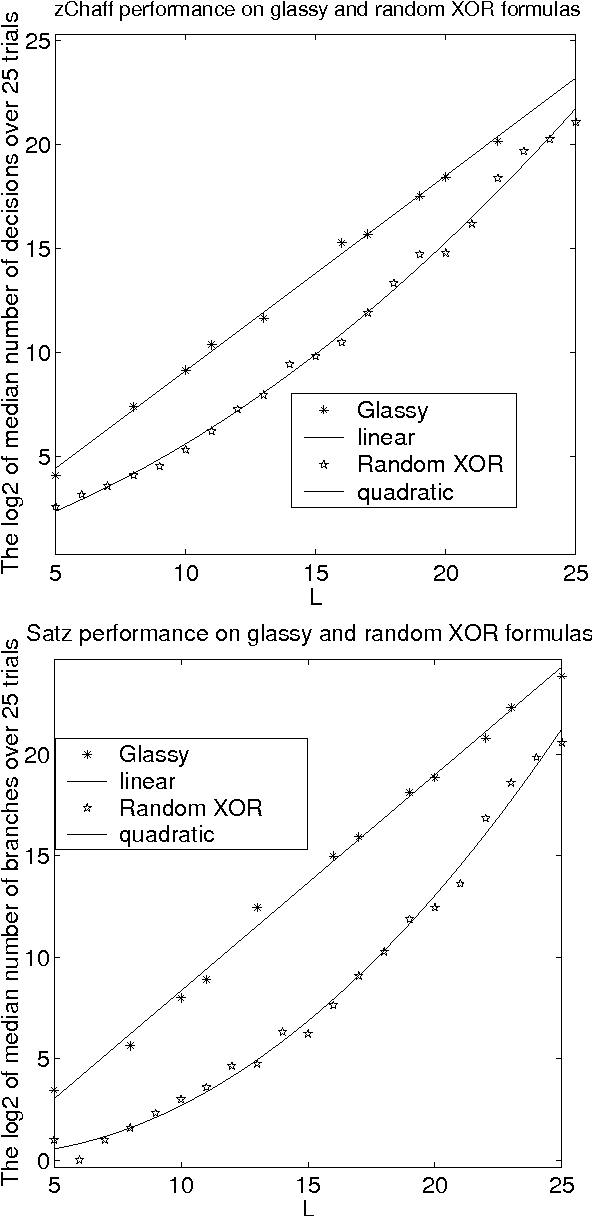
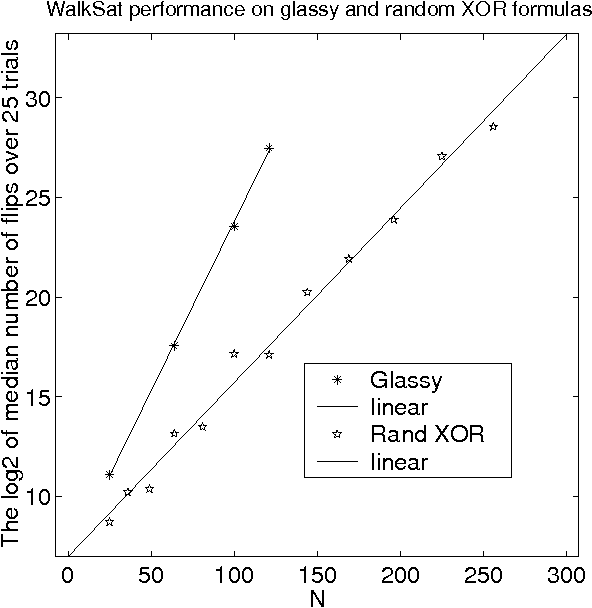
Abstract:We introduce a highly structured family of hard satisfiable 3-SAT formulas corresponding to an ordered spin-glass model from statistical physics. This model has provably "glassy" behavior; that is, it has many local optima with large energy barriers between them, so that local search algorithms get stuck and have difficulty finding the true ground state, i.e., the unique satisfying assignment. We test the hardness of our formulas with two Davis-Putnam solvers, Satz and zChaff, the recently introduced Survey Propagation (SP), and two local search algorithms, Walksat and Record-to-Record Travel (RRT). We compare our formulas to random 3-XOR-SAT formulas and to two other generators of hard satisfiable instances, the minimum disagreement parity formulas of Crawford et al., and Hirsch's hgen. For the complete solvers the running time of our formulas grows exponentially in sqrt(n), and exceeds that of random 3-XOR-SAT formulas for small problem sizes. SP is unable to solve our formulas with as few as 25 variables. For Walksat, our formulas appear to be harder than any other known generator of satisfiable instances. Finally, our formulas can be solved efficiently by RRT but only if the parameter d is tuned to the height of the barriers between local minima, and we use this parameter to measure the barrier heights in random 3-XOR-SAT formulas as well.
Hiding Satisfying Assignments: Two are Better than One
Mar 20, 2005
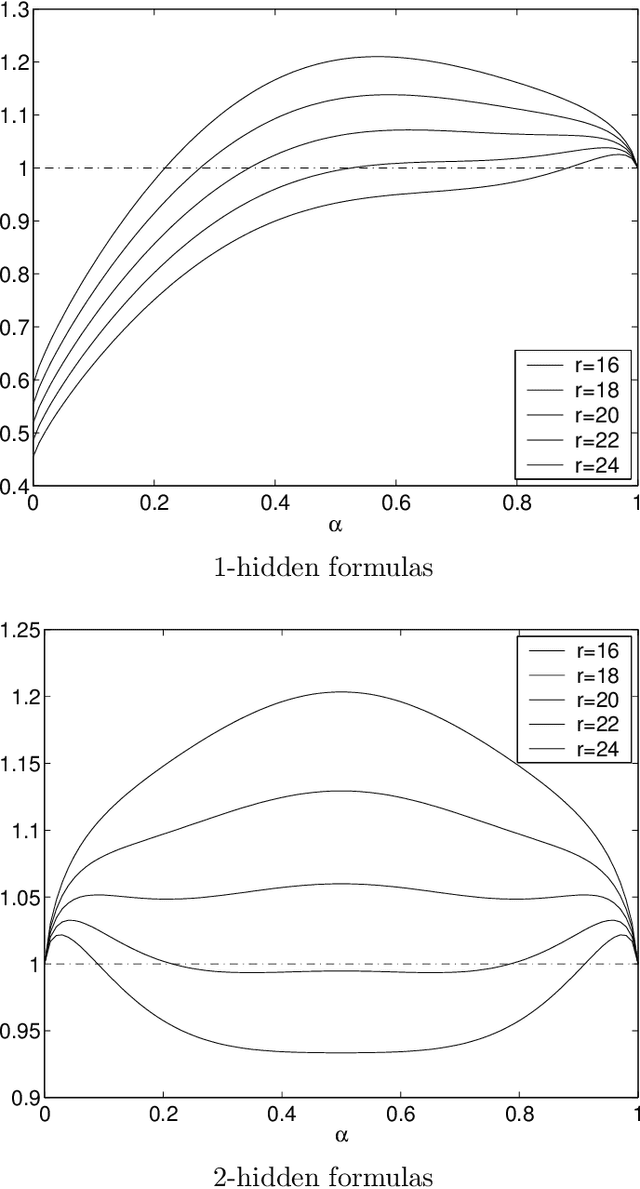
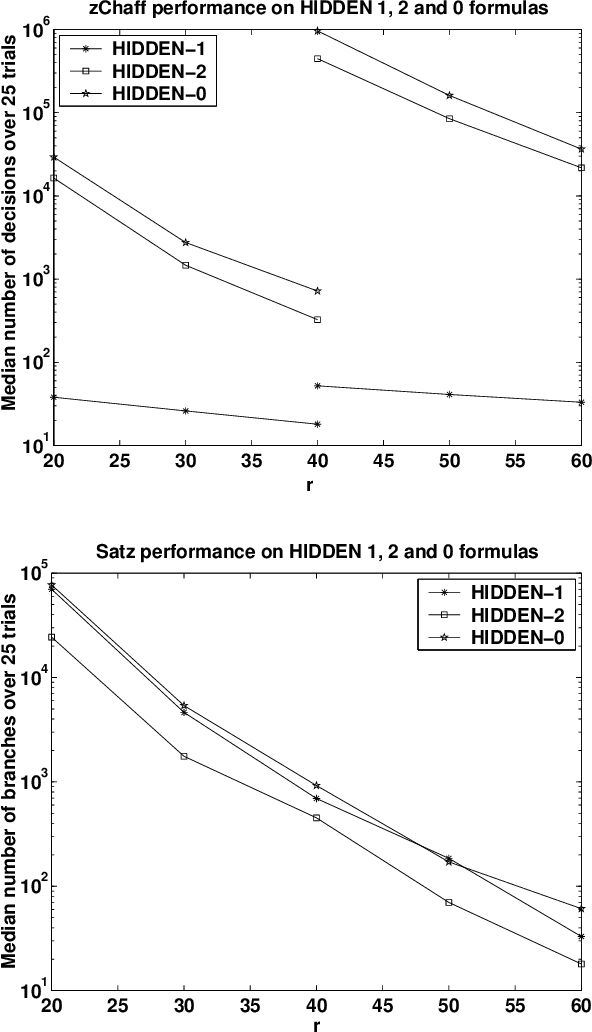
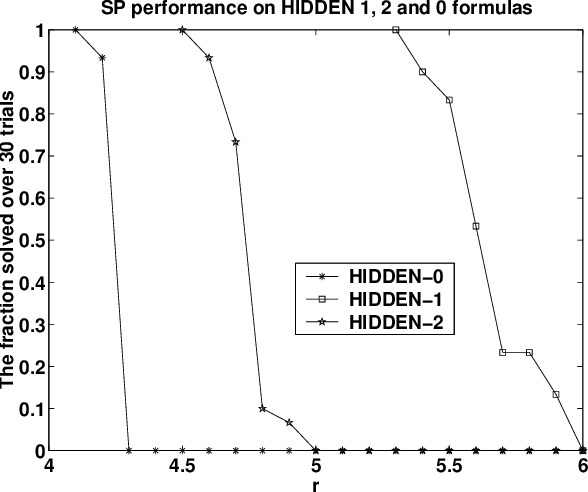
Abstract:The evaluation of incomplete satisfiability solvers depends critically on the availability of hard satisfiable instances. A plausible source of such instances consists of random k-SAT formulas whose clauses are chosen uniformly from among all clauses satisfying some randomly chosen truth assignment A. Unfortunately, instances generated in this manner tend to be relatively easy and can be solved efficiently by practical heuristics. Roughly speaking, as the formula's density increases, for a number of different algorithms, A acts as a stronger and stronger attractor. Motivated by recent results on the geometry of the space of satisfying truth assignments of random k-SAT and NAE-k-SAT formulas, we introduce a simple twist on this basic model, which appears to dramatically increase its hardness. Namely, in addition to forbidding the clauses violated by the hidden assignment A, we also forbid the clauses violated by its complement, so that both A and complement of A are satisfying. It appears that under this "symmetrization'' the effects of the two attractors largely cancel out, making it much harder for algorithms to find any truth assignment. We give theoretical and experimental evidence supporting this assertion.
Generating Hard Satisfiable Formulas by Hiding Solutions Deceptively
Mar 18, 2005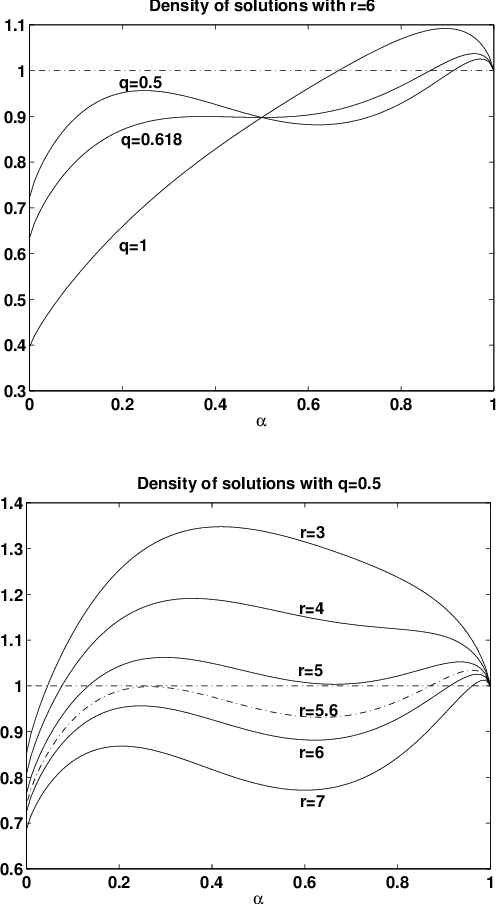
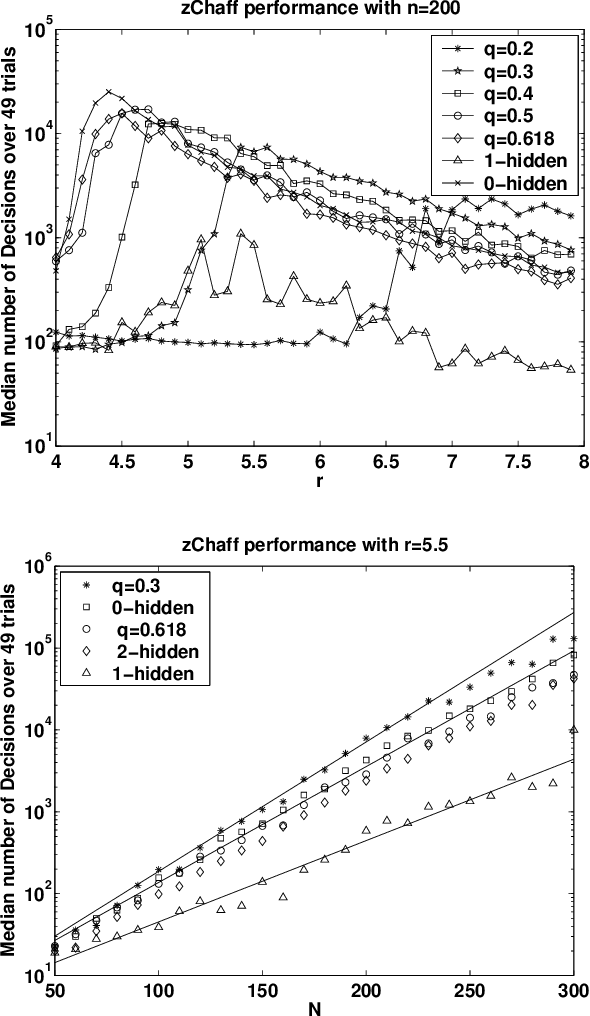
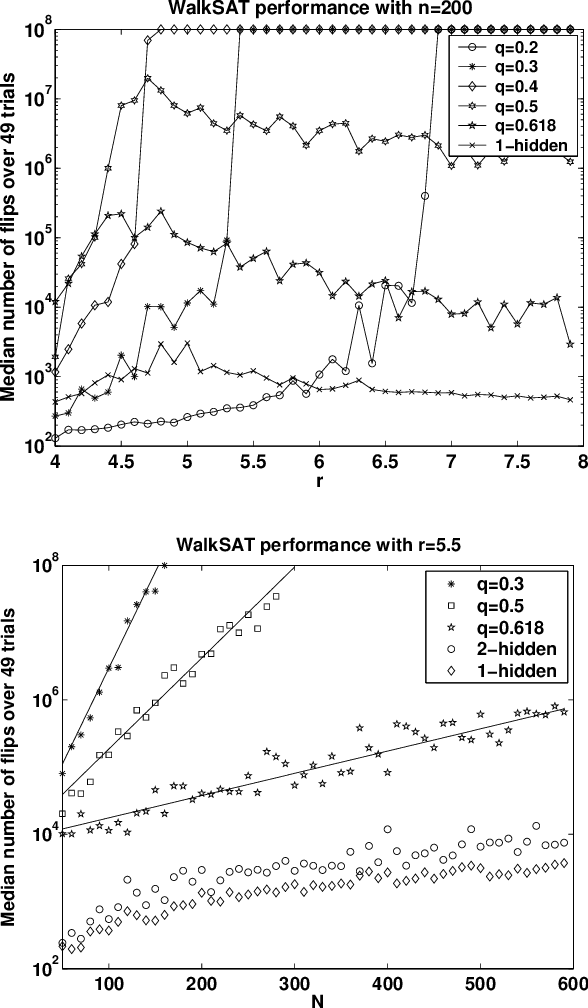
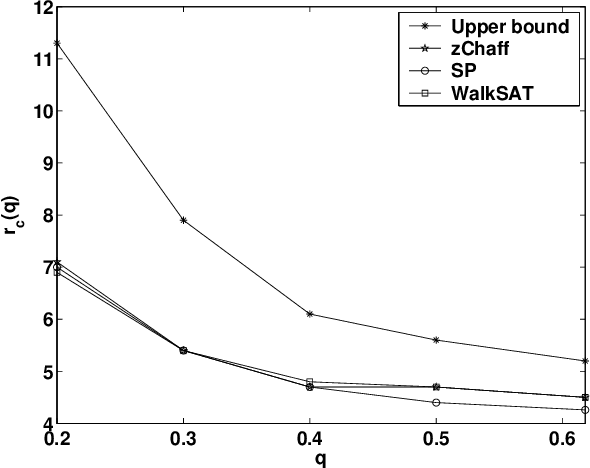
Abstract:To test incomplete search algorithms for constraint satisfaction problems such as 3-SAT, we need a source of hard, but satisfiable, benchmark instances. A simple way to do this is to choose a random truth assignment A, and then choose clauses randomly from among those satisfied by A. However, this method tends to produce easy problems, since the majority of literals point toward the ``hidden'' assignment A. Last year, Achlioptas, Jia and Moore proposed a problem generator that cancels this effect by hiding both A and its complement. While the resulting formulas appear to be just as hard for DPLL algorithms as random 3-SAT formulas with no hidden assignment, they can be solved by WalkSAT in only polynomial time. Here we propose a new method to cancel the attraction to A, by choosing a clause with t > 0 literals satisfied by A with probability proportional to q^t for some q < 1. By varying q, we can generate formulas whose variables have no bias, i.e., which are equally likely to be true or false; we can even cause the formula to ``deceptively'' point away from A. We present theoretical and experimental results suggesting that these formulas are exponentially hard both for DPLL algorithms and for incomplete algorithms such as WalkSAT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge