Be Persistent: Towards a Unified Solution for Mitigating Shortcuts in Deep Learning

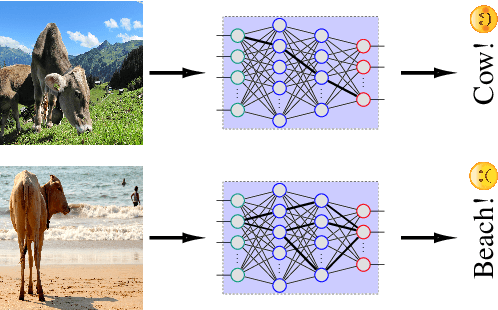
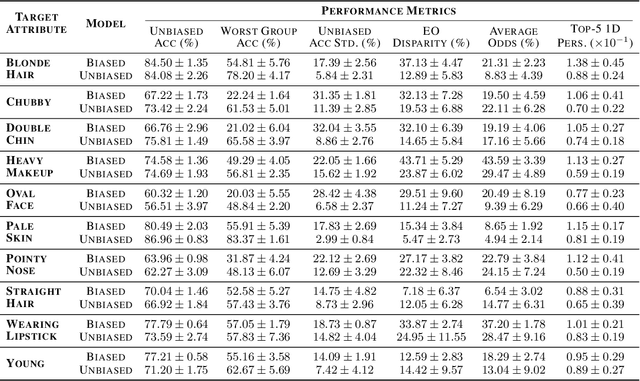
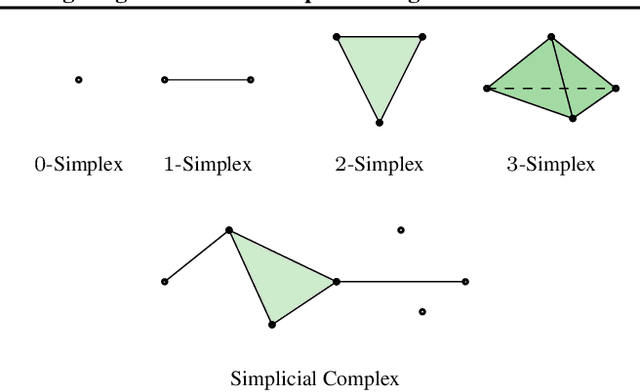
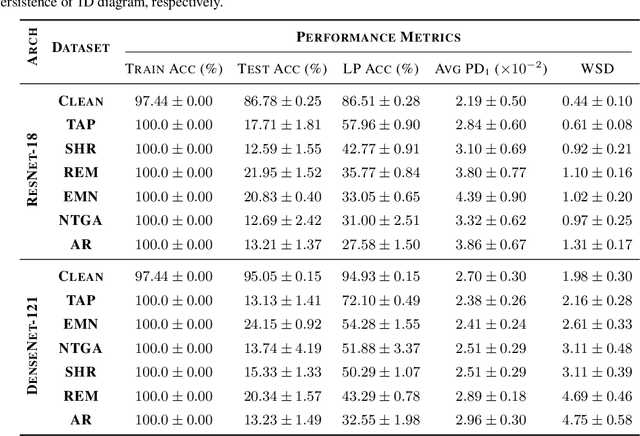
Deep neural networks (DNNs) are vulnerable to shortcut learning: rather than learning the intended task, they tend to draw inconclusive relationships between their inputs and outputs. Shortcut learning is ubiquitous among many failure cases of neural networks, and traces of this phenomenon can be seen in their generalizability issues, domain shift, adversarial vulnerability, and even bias towards majority groups. In this paper, we argue that this commonality in the cause of various DNN issues creates a significant opportunity that should be leveraged to find a unified solution for shortcut learning. To this end, we outline the recent advances in topological data analysis~(TDA), and persistent homology~(PH) in particular, to sketch a unified roadmap for detecting shortcuts in deep learning. We demonstrate our arguments by investigating the topological features of computational graphs in DNNs using two cases of unlearnable examples and bias in decision-making as our test studies. Our analysis of these two failure cases of DNNs reveals that finding a unified solution for shortcut learning in DNNs is not out of reach, and TDA can play a significant role in forming such a framework.

The Devil's Advocate: Shattering the Illusion of Unexploitable Data using Diffusion Models

Protecting personal data against the exploitation of machine learning models is of paramount importance. Recently, availability attacks have shown great promise to provide an extra layer of protection against the unauthorized use of data to train neural networks. These methods aim to add imperceptible noise to clean data so that the neural networks cannot extract meaningful patterns from the protected data, claiming that they can make personal data "unexploitable." In this paper, we provide a strong countermeasure against such approaches, showing that unexploitable data might only be an illusion. In particular, we leverage the power of diffusion models and show that a carefully designed denoising process can defuse the ramifications of the data-protecting perturbations. We rigorously analyze our algorithm, and theoretically prove that the amount of required denoising is directly related to the magnitude of the data-protecting perturbations. Our approach, called AVATAR, delivers state-of-the-art performance against a suite of recent availability attacks in various scenarios, outperforming adversarial training. Our findings call for more research into making personal data unexploitable, showing that this goal is far from over.

COLLIDER: A Robust Training Framework for Backdoor Data

Deep neural network (DNN) classifiers are vulnerable to backdoor attacks. An adversary poisons some of the training data in such attacks by installing a trigger. The goal is to make the trained DNN output the attacker's desired class whenever the trigger is activated while performing as usual for clean data. Various approaches have recently been proposed to detect malicious backdoored DNNs. However, a robust, end-to-end training approach, like adversarial training, is yet to be discovered for backdoor poisoned data. In this paper, we take the first step toward such methods by developing a robust training framework, COLLIDER, that selects the most prominent samples by exploiting the underlying geometric structures of the data. Specifically, we effectively filter out candidate poisoned data at each training epoch by solving a geometrical coreset selection objective. We first argue how clean data samples exhibit (1) gradients similar to the clean majority of data and (2) low local intrinsic dimensionality (LID). Based on these criteria, we define a novel coreset selection objective to find such samples, which are used for training a DNN. We show the effectiveness of the proposed method for robust training of DNNs on various poisoned datasets, reducing the backdoor success rate significantly.

Adversarial Coreset Selection for Efficient Robust Training

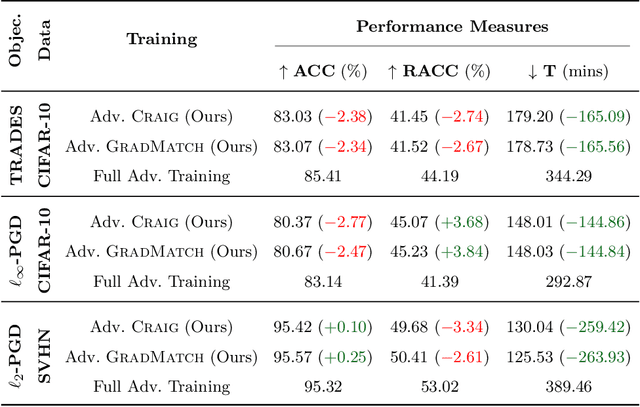
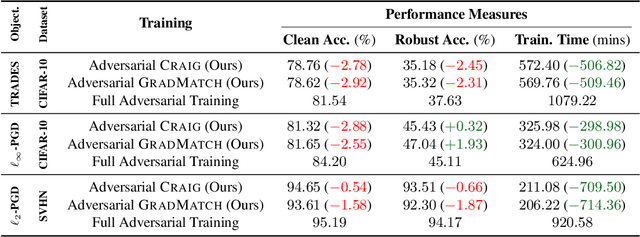
Neural networks are vulnerable to adversarial attacks: adding well-crafted, imperceptible perturbations to their input can modify their output. Adversarial training is one of the most effective approaches to training robust models against such attacks. Unfortunately, this method is much slower than vanilla training of neural networks since it needs to construct adversarial examples for the entire training data at every iteration. By leveraging the theory of coreset selection, we show how selecting a small subset of training data provides a principled approach to reducing the time complexity of robust training. To this end, we first provide convergence guarantees for adversarial coreset selection. In particular, we show that the convergence bound is directly related to how well our coresets can approximate the gradient computed over the entire training data. Motivated by our theoretical analysis, we propose using this gradient approximation error as our adversarial coreset selection objective to reduce the training set size effectively. Once built, we run adversarial training over this subset of the training data. Unlike existing methods, our approach can be adapted to a wide variety of training objectives, including TRADES, $\ell_p$-PGD, and Perceptual Adversarial Training. We conduct extensive experiments to demonstrate that our approach speeds up adversarial training by 2-3 times while experiencing a slight degradation in the clean and robust accuracy.

$\ell_\infty$-Robustness and Beyond: Unleashing Efficient Adversarial Training

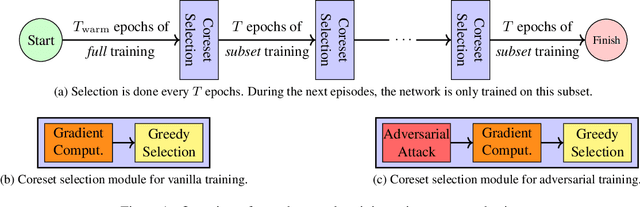
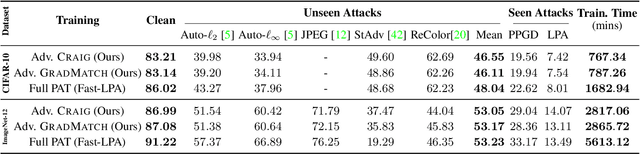
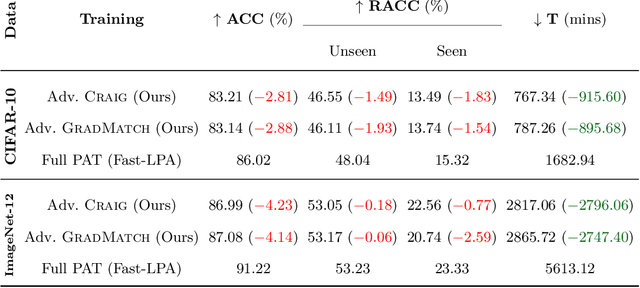
Neural networks are vulnerable to adversarial attacks: adding well-crafted, imperceptible perturbations to their input can modify their output. Adversarial training is one of the most effective approaches in training robust models against such attacks. However, it is much slower than vanilla training of neural networks since it needs to construct adversarial examples for the entire training data at every iteration, which has hampered its effectiveness. Recently, Fast Adversarial Training was proposed that can obtain robust models efficiently. However, the reasons behind its success are not fully understood, and more importantly, it can only train robust models for $\ell_\infty$-bounded attacks as it uses FGSM during training. In this paper, by leveraging the theory of coreset selection we show how selecting a small subset of training data provides a more principled approach towards reducing the time complexity of robust training. Unlike existing methods, our approach can be adapted to a wide variety of training objectives, including TRADES, $\ell_p$-PGD, and Perceptual Adversarial Training. Our experimental results indicate that our approach speeds up adversarial training by 2-3 times, while experiencing a small reduction in the clean and robust accuracy.

AdvFlow: Inconspicuous Black-box Adversarial Attacks using Normalizing Flows

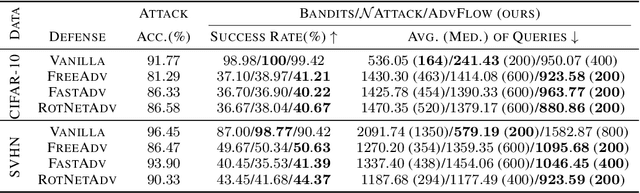
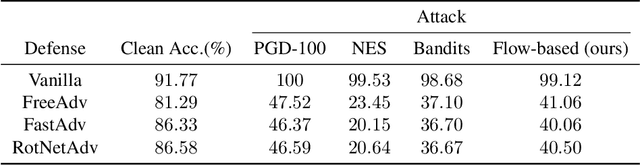
Deep learning classifiers are susceptible to well-crafted, imperceptible variations of their inputs, known as adversarial attacks. In this regard, the study of powerful attack models sheds light on the sources of vulnerability in these classifiers, hopefully leading to more robust ones. In this paper, we introduce AdvFlow: a novel black-box adversarial attack method on image classifiers that exploits the power of normalizing flows to model the density of adversarial examples around a given target image. We see that the proposed method generates adversaries that closely follow the clean data distribution, a property which makes their detection less likely. Also, our experimental results show competitive performance of the proposed approach with some of the existing attack methods on defended classifiers, outperforming them in both the number of queries and attack success rate. The code is available at https://github.com/hmdolatabadi/AdvFlow.

Black-box Adversarial Example Generation with Normalizing Flows

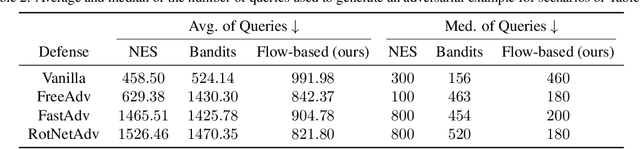
Deep neural network classifiers suffer from adversarial vulnerability: well-crafted, unnoticeable changes to the input data can affect the classifier decision. In this regard, the study of powerful adversarial attacks can help shed light on sources of this malicious behavior. In this paper, we propose a novel black-box adversarial attack using normalizing flows. We show how an adversary can be found by searching over a pre-trained flow-based model base distribution. This way, we can generate adversaries that resemble the original data closely as the perturbations are in the shape of the data. We then demonstrate the competitive performance of the proposed approach against well-known black-box adversarial attack methods.

Invertible Generative Modeling using Linear Rational Splines

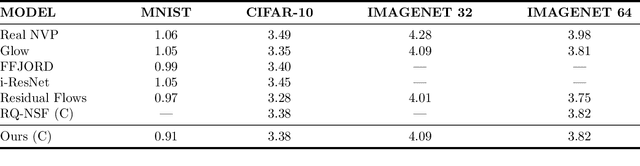
Normalizing flows attempt to model an arbitrary probability distribution through a set of invertible mappings. These transformations are required to achieve a tractable Jacobian determinant that can be used in high-dimensional scenarios. The first normalizing flow designs used coupling layer mappings built upon affine transformations. The significant advantage of such models is their easy-to-compute inverse. Nevertheless, making use of affine transformations may limit the expressiveness of such models. Recently, invertible piecewise polynomial functions as a replacement for affine transformations have attracted attention. However, these methods require solving a polynomial equation to calculate their inverse. In this paper, we explore using linear rational splines as a replacement for affine transformations used in coupling layers. Besides having a straightforward inverse, inference and generation have similar cost and architecture in this method. Moreover, simulation results demonstrate the competitiveness of this approach's performance compared to existing methods.